pomocy
Sajek.: Pomocy.!
Jak narysować wykres funkcji: y= f(|x|)
Proszę pomóżcie mi ktoś. !
6 gru 21:57
Rudy: Dla argumentów dodatnich jest to samo co f(x), dla argumentów ujemnych jest lustrzane odbicie
tego co dla dodatnich czyli w symetrii względem osi Oy
6 gru 21:59
onaa:
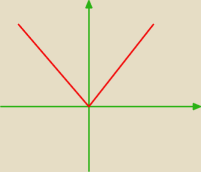
nie jestem pewna ale to chyba tak...
6 gru 22:00
onaa: linie czerwone są do siebie symetryczne względem OY
6 gru 22:01
dante:
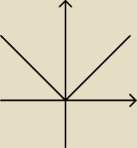
6 gru 22:02
dante:
6 gru 22:03
matthew: y= f(|x|)
− likwiduje lewą część wykresu
− na to miejsce odbija symetrycznie prawą część
6 gru 22:04
Rudy: To co narysowała onaa to wykres konkretnej funkcji y=f(x)=|x|
To o co pyta Sajek to przekształcenie funkcji f(x) która jest nieokreślona konkretnie, można
taką operację zastosować do dowolnej funkcji robiąc z jej wykresem to soco napisałem wcześniej
6 gru 22:04
joker_89:
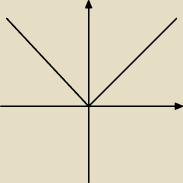
wykres będzie wyglądał mniej więcej tak, wystarczy, że zrobisz sobie tabelkę i dla każdego
argumentu x policzysz jego wartość y czyli na przykład jeśli x=−1 to y=1, jeśli x=−2 to y=2,
jeśli x=1 to y=1 itd.
6 gru 22:04
Rudy: a można to zapisać tak:
y=f(|x|)= f(x) dla x≥0;
f(−x) dla x<0
6 gru 22:06
Nikka: czy można narysować wykres funkcji nie znając jej wzoru ...
wykres przedstawia wzór funkcji y = |x|
a w zadaniu jest f(|x|)... gdyby f(x) = x
2 to f(|x|) = (|x|)
2= x
2
czy ja dobrze myślę...
6 gru 22:07
Rudy: Myślę że tu może być w zapisie który podał Sajek. Może chodzić po prostu o y=|x|, a nie o
y=f(|x|)
Sajek sprawdź treść zadania popraw jeśli nie o to chodzi.
6 gru 22:08
Rudy: No właśnie o to chodzi Nikka, można opisać co zrobić z wykresem funkcji f(x) ale póki nie wiemy
jaka to funkcja narysować się jej nie da
6 gru 22:09
Sajek.: Aha dzieki
a to w takiem razie pomozecie mi jescze jak narysowac taki wykres: y=|f(|x|)|
6 gru 22:09
Rudy: Najpierw powiedz jaką funkcję f(x) będziemy przekształcać
6 gru 22:09
onaa: mi się wydaj, że tu chodzi ogółem o samo rozumienie jak będzie wyglądać taka funkcja w module.
tez to miałam na lekcjach i to właśnie pod tym kątem jest zadanie a nie na przekształcanie
konkretnego wzoru funkcji...
6 gru 22:12
Rudy: No to najpierw część wykresu po lewej stronie osi Oy jest kasowana, w jej miejsce odbija się
lustrzanie prawą stronę wykresu. Potem wszystko co jest pod osią Ox jest lustrzanie odbijane
do góry, ponad oś Ox.
Czyli najpierw symetria wzgl. osi Oy dla x≥0
Potem symetria wzgl. osi Ox dla y<0
6 gru 22:17
Sajek.:
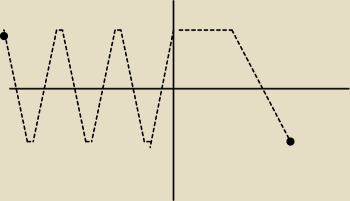
mam problemy z jej narysowaniem
ona wyglada mniej wiecej w taki sposób: tyle ze :f:<−8;4>−>R
Tu mi sie nie zmieściła cala na wykresie
6 gru 22:17
Rudy: Oczywiście mówię o przykładzie y=|f(|x|)|
6 gru 22:18
Sajek.: Sory nie potrafie go narysować dokladnie
I wykres nie jest rysowany ciągłą linią.
6 gru 22:18
Sajek.: Sory: JEST RYSOWANY CIĄGŁĄ LINIĄ.
Tak, wykres się tyczy obydwu przkładów o które chcę się dowiedzieć.
6 gru 22:19
Rudy:
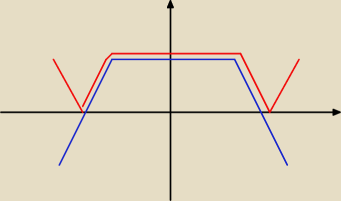
6 gru 22:20
Rudy: Najpierw to niebieskie
Potem czerwone, oczywiście linie się pokrywają a nie są obok siebie, narysowałem obok żeby było
widać po kolei operacje na wykresie
6 gru 22:21
Sajek.: Nie rozumiem zbytnio
Czyli wszystko co jest pod osią X ma zostać odwrócone względem niej?
6 gru 22:24
Bogdan:
Pytanie (Sajek): "jak narysować wykres funkcji: y= f(|x|) ?"
Odpowiedź (Rudy z drobnym uzupełnieniem): "dla argumentów dodatnich lub dla x = 0
jest to samo co f(x), dla argumentów ujemnych jest lustrzane odbicie tego, co dla dodatnich,
czyli w symetrii względem osi y".
Tę odpowiedź można przyjąć jako wyczerpującą temat, bo zawiera przepis na narysowanie
wykresu y = f(|x|).
6 gru 22:24
Sajek.: Ten przyklad rozumiem.
A odnosnie tego: y=|f(|x|)| może mi ktoś jeszcze raz wytłumaczyć?
6 gru 22:28
Bogdan:
A sam jak to widzisz?
Znasz przecież przekształcenie wykresu y = f(x) w wykres y = |f(x)| oraz tu omówione
przekształcenie wykresu y = f(x) w wykres y = f(|x|).
6 gru 22:38
onaa: czy możecie zajrzeć do moich zadań? błagam:(
6 gru 22:39
Sajek.: okk.dzieki wielkie wszystkim za pomoc.
6 gru 22:44
tomek: y=x+1
8 kwi 18:53