| x | x | π | ||||
obliczyć sin | i cos | jeśli tgx=0,75 i x∊(0; | ) | |||
| 2 | 2 | 2 |
| 2tgx | x | |||
Trzeba zastosować tu wzór tg2x= | i za jego pomocą obliczyć tg | |||
| 1 − tg2x | 2 |
| 4 | ||
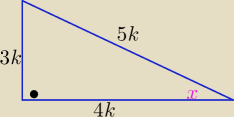
kąt x −− ostry to cosx= | ||
| 5 |
| x | x | 9 | x | 3√10 | ||||||
i cosx= 2cos2 | −1 ⇒ cos2 | = | ⇒ cos | =+ | ||||||
| 2 | 2 | 10 | 2 | 10 |
| x | 9 | √10 | ||||
to sin | = √1− | = + | ||||
| 2 | 10 | 10 |
| 5^2 | 52 |
| 2^{10} | 210 |
| a_2 | a2 |
| a_{25} | a25 |
| p{2} | √2 |
| p{81} | √81 |
| Kliknij po więcej przykładów | |
|---|---|
| Twój nick | |