aa
Hugo: Dane jest zdanie
jeżeli pan Jan sklamal lub Piotr skamal to jeżeli Jan nie sklamal to Piotr sklamal
P − Piostr
J − Jan
~ skamal
(~J v ~P ) −> (J −>~P)
tak

?
26 cze 17:23
Hugo: b) zbadaj czy jest prawdziwe
aby implikacja byla nieprawdziwa to musi być 1−>0
(~J v ~P ) (prawdziwe) a (J −>~P) (fałsz)
(~J v ~P ) bedzie nie prawdziwe dla J = 1 i P = 1 , (J −>~P) bedzie nieprawdziwe gdy J =1 i P
= 1
jedyną kombinacją aby prawa strona była fałszywa to P = 1 i J = 1, podstawiamy do lewej cześci
równania
(~1 v ~1) = (0 v 0 ) = 0
Końcowy wynik to
0 −> 0 a to jest zawsze prawdą

26 cze 18:01
Trivial:
Możesz też uprościć to algebraicznie:
a = ~J, b = ~P
(a+b) → (~a → b) = (a+b) → (a+b) = 1.
26 cze 18:24
Hugo:
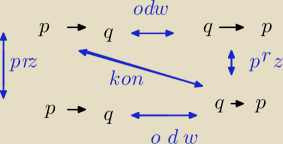
c) Zapisz zaprzeczenie tego zdania
~[ (~J v ~P ) −> (J −>~P) ] <=> (~J v ~P ) i ~(J −>~P) <=> (~J v ~P ) i ( J i P )
d) zapisz kontrapozycja zdania początkowego
kontrapozycja[ (~J v ~P ) −> (J −>~P) ] i tu troche nie wiem

odwróce wpierw?
(J −>~P) −> (~J v ~P ) i teraz to zaprzecze
(J −>~P) i ~(~J v ~P) <=> (J −>~P) i ( J i P)
26 cze 18:30
Hugo: Trivial wole przy swoim

26 cze 18:36
Hugo: ale ogólnie dobrze? w pon pisze egzamin z dyskretnej

26 cze 18:37
Hugo: Czy istnieje kontrprzyklad do zdania (kopnięte A to chyba to samo co V) Vx1, x2 ∊ Zn((x1 =/=
0 i x2 =/= 0) => x1x2 =0)
26 cze 18:38
Hugo:
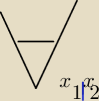
26 cze 18:39
Hugo: na odwót
ale nie ma obróconego 'V'

ostatecznie: Dla każdego x
1 , x
2 ∊ Zn((x1 =/=0 i x
2 =/= 0) => x
1x
2 =0)
26 cze 18:42
Hugo: Zn to całkowite naturalne?
26 cze 18:43
Hugo: jeżeli x
1 i x
2 nie mogą być zerami

to nie można wymnożyc tak by wyszło zero
26 cze 18:44
Hugo: odp Nie da się?
26 cze 18:44
Hugo: G − W
8. Odwiedź z uzasadnieniem na poniższe pytania
a) czy G jest hamiltonowski
b) Czy G jest eulerowski
c) Podaj lambda(G) oraz kappa(G)
d) podaj x(G) i x'(G)
e) Narysuj drzewo spinające i podaj gamma(G) i ksi* (G)
jaki to jest graf W
8


pelny

26 cze 18:51
Hugo:
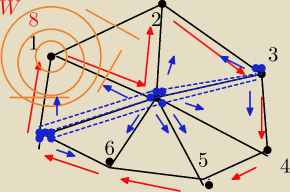
taki

?
a) czy G jest hamiltonowski
b) Czy G jest eulerowski
c) Podaj lambda(G) oraz kappa(G)
d) podaj x(G) i x'(G)
e) Narysuj drzewo spinające i podaj gamma(G) i ksi* (G)
hamiltonowski musi być spójny & cykl Hamiltona , cykl Hamiltona to bylo że wierzchołki muszą
tworzyc cykl i sie nie powtarzać poza pierwszym V
p = V
k
zawiera

? wychodzi mi że tak
b) Czy jest eulerowski, czyli to samo tylko ze dla krawędzi
z twierdzenia to zeby był eulerowski wierzchołki muszą mieć parzysty stopnień

czyli sie nie da

c) Podaj lambda(G) oraz kappa(G)
Lambda (G) ilosc krawędzi minimalna by graf nie był spójny
kappa(G) il. wierzchołków .... wraz z krawędziami indencydentalnymi *
Lambda(G) = 3  kappa(G) = 3
kappa(G) = 3 
też
26 cze 19:12
Hugo:
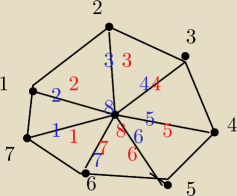
d) podaj x(G) i x'(G)
liczba chromatyczna x(G) − wierzchołki min. ilosc kolorów by pomalowac = 8
indeks chromatyczny x'(G) − min. ilosc kolorów by pomalowac krawędzie = 8
26 cze 19:18
Hugo: e)
Drzewo rozpinające (ang. Spanning Tree) – drzewo, które zawiera wszystkie wierzchołki grafu G,
zaś zbiór krawędzi drzewa jest podzbiorem zbioru krawędzi grafu.
Narysuj drzewo spinające i podaj gamma(G) i ksi* (G)
ta liczba cykloidalna to było gamma(G) = m−n+k
ksi (G) = n−k
26 cze 19:24
Hugo: jak to zrobic


26 cze 19:43
 ?
?

 c) Zapisz zaprzeczenie tego zdania
~[ (~J v ~P ) −> (J −>~P) ] <=> (~J v ~P ) i ~(J −>~P) <=> (~J v ~P ) i ( J i P )
d) zapisz kontrapozycja zdania początkowego
kontrapozycja[ (~J v ~P ) −> (J −>~P) ] i tu troche nie wiem
c) Zapisz zaprzeczenie tego zdania
~[ (~J v ~P ) −> (J −>~P) ] <=> (~J v ~P ) i ~(J −>~P) <=> (~J v ~P ) i ( J i P )
d) zapisz kontrapozycja zdania początkowego
kontrapozycja[ (~J v ~P ) −> (J −>~P) ] i tu troche nie wiem odwróce wpierw?
(J −>~P) −> (~J v ~P ) i teraz to zaprzecze
(J −>~P) i ~(~J v ~P) <=> (J −>~P) i ( J i P)
odwróce wpierw?
(J −>~P) −> (~J v ~P ) i teraz to zaprzecze
(J −>~P) i ~(~J v ~P) <=> (J −>~P) i ( J i P)


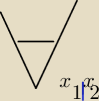
 ostatecznie: Dla każdego x1 , x2 ∊ Zn((x1 =/=0 i x2 =/= 0) => x1x2 =0)
ostatecznie: Dla każdego x1 , x2 ∊ Zn((x1 =/=0 i x2 =/= 0) => x1x2 =0)
 to nie można wymnożyc tak by wyszło zero
to nie można wymnożyc tak by wyszło zero



 pelny
pelny
 taki
taki  ?
a) czy G jest hamiltonowski
b) Czy G jest eulerowski
c) Podaj lambda(G) oraz kappa(G)
d) podaj x(G) i x'(G)
e) Narysuj drzewo spinające i podaj gamma(G) i ksi* (G)
hamiltonowski musi być spójny & cykl Hamiltona , cykl Hamiltona to bylo że wierzchołki muszą
tworzyc cykl i sie nie powtarzać poza pierwszym Vp = Vk
zawiera
?
a) czy G jest hamiltonowski
b) Czy G jest eulerowski
c) Podaj lambda(G) oraz kappa(G)
d) podaj x(G) i x'(G)
e) Narysuj drzewo spinające i podaj gamma(G) i ksi* (G)
hamiltonowski musi być spójny & cykl Hamiltona , cykl Hamiltona to bylo że wierzchołki muszą
tworzyc cykl i sie nie powtarzać poza pierwszym Vp = Vk
zawiera  ? wychodzi mi że tak
b) Czy jest eulerowski, czyli to samo tylko ze dla krawędzi
z twierdzenia to zeby był eulerowski wierzchołki muszą mieć parzysty stopnień
? wychodzi mi że tak
b) Czy jest eulerowski, czyli to samo tylko ze dla krawędzi
z twierdzenia to zeby był eulerowski wierzchołki muszą mieć parzysty stopnień  czyli sie nie da
czyli sie nie da c) Podaj lambda(G) oraz kappa(G)
Lambda (G) ilosc krawędzi minimalna by graf nie był spójny
kappa(G) il. wierzchołków .... wraz z krawędziami indencydentalnymi *
Lambda(G) = 3
c) Podaj lambda(G) oraz kappa(G)
Lambda (G) ilosc krawędzi minimalna by graf nie był spójny
kappa(G) il. wierzchołków .... wraz z krawędziami indencydentalnymi *
Lambda(G) = 3  kappa(G) = 3
kappa(G) = 3  też
też
 d) podaj x(G) i x'(G)
liczba chromatyczna x(G) − wierzchołki min. ilosc kolorów by pomalowac = 8
indeks chromatyczny x'(G) − min. ilosc kolorów by pomalowac krawędzie = 8
d) podaj x(G) i x'(G)
liczba chromatyczna x(G) − wierzchołki min. ilosc kolorów by pomalowac = 8
indeks chromatyczny x'(G) − min. ilosc kolorów by pomalowac krawędzie = 8

