Ekstrema i monotoniczność, przegiecie i wypukłość
Klaudia: Ekstrema lokalne i monotoniczność funkcji:
Pkt. przegięcia i zbadać wypukłość funkcji:
f(x)1−ln(x
2−4)
26 cze 14:39
J:
i nie wiesz od czego zacząć ?
26 cze 14:40
Klaudia: nie wiem jak zacząć skończyć i w ogóle xD
26 cze 14:42
J:
trzeba policzyć pochodną ... potrafisz ?
26 cze 14:45
Klaudia: No pochodne wiem jak liczyć ale dla sprawdzenia czy dobrze to policze wolę miec to rozpisane
26 cze 14:49
J:
pokaż pochodną
26 cze 14:50
26 cze 14:56
J:
nie .. zastosuj wzór na pochodną ilorazu funkcji
26 cze 15:07
Klaudia: | (x2)'*(x−2)−(x2)(*x−2)' | |
| |
| (x−2)2 | |
26 cze 15:16
J:
dokładnie tak ... teraz to policz
26 cze 15:17
Klaudia: | 2x*(x−2)−(x2)*(−2) | | 2x2−4−2x2 | |
| = |
| |
| x2−2x+4 | | x2−2x+4 | |
26 cze 15:18
J:
ile jest pochodna z: x − 2 ?
26 cze 15:20
Klaudia: 1
26 cze 15:21
J:
no ... a u Ciebie : −2 .... popraw
26 cze 15:24
Klaudia: | 2x*(x−2)−(x2)*(1) | | 2x2−4x−x2 | |
| = |
| |
| x2−2x+4 | | x2−2x+4 | |
26 cze 15:27
J:
| | x2 − 4x | |
dobra ... f'(x) = |
| .. teraz kiedy ta pochodna się zeruje ? |
| | (x−2)2 | |
26 cze 15:28
Klaudia: x=0

teraz to nie jestem pewna czy dobrze myśle
26 cze 15:30
J:
x(x−4) = 0 ⇔ x = 0 lub x = 4 ..... warunek konieczny ekstremum ..
warunek wystarczający zmiana znaku pochodnej w tych punktach ...
potarfisz naszkicować wykres licznika pochodnej (bo tylko od niego zależy jej znak)
f(x) = x2 − 4x
26 cze 15:34
Klaudia:
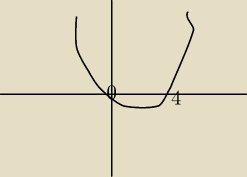
26 cze 15:42
J:
dobra ... pochodna zmienia znak , czyli mamy dwa ekstrema ...
teraz ... gdy pochodna jest dodatnia , to funkcja jest rosnąca, gdy ujemna to malejąca ..
ustal te przedziały i będziesz miała monotoniczność i ekstrema..
26 cze 15:45
Klaudia: f↗ (−∞,0) (4,+∞)
f↘ (0,4) tak to będzie?
26 cze 15:48
J:
perfect ...

.. jeszcze tylko określ ekstrema .. dla x = 0 mamy ...? , dla x = 4 ...?
26 cze 15:51
J:
I na początku wyznacz dziedzinę funkcji... x − 2 ≠ 0 ⇔ .... ?
26 cze 15:52
Klaudia: f(0)=0
f(4)=0
?
26 cze 15:55
J:
pytam , gdzie jest maksimum, a gdzie minimum ?
26 cze 15:56
Klaudia: nie wiem jak to zrobić
26 cze 15:57
J:
jak x idzie od − ∞ do 0 , to funkcja rośnie , a jak minie 0 , to maleje ..
zatem w punkcie x = 0 osiąga ...?
26 cze 15:58
J:
muszę kończyć ... .to samo przeanalizuj dla punktu: x = 4
26 cze 15:59
Klaudia: ok jeszcze przeanalizuje

wielkie dzięki za pomoc

26 cze 16:00
 teraz to nie jestem pewna czy dobrze myśle
teraz to nie jestem pewna czy dobrze myśle

 .. jeszcze tylko określ ekstrema .. dla x = 0 mamy ...? , dla x = 4 ...?
.. jeszcze tylko określ ekstrema .. dla x = 0 mamy ...? , dla x = 4 ...?
 wielkie dzięki za pomoc
wielkie dzięki za pomoc 