trygonometria
bimbam: oblicz zbiór wartości
y=1−cos(2x)
Odp <−1;1>
Jeżeli cos(2x)=2cos
2x−1
to 1−2cos
2x+1
−1≤cos
2x+2≤1 i cosx=t
wychodzi mi
2−2t
2≤1 lub −2t
2+3≥0
2t
2≥1 Δ=24 t∊<−
√2/2;
√2/2>
t∊(−
∞; −
√2/2 > u <
√2/2; +
∞)
No nie wiem jak to zrobić

25 cze 06:17
J:
− 1 ≤ cosx ≤ 1
− 1 ≤ cos2x ≤ 1
1 ≥ − cos2x ≥ −1
1 + 1 ≥ 1 − cos2x ≥ −1 +1
2 ≥ 1 − cos2x ≥ 0
Zw = [0,2]
25 cze 08:21
J:
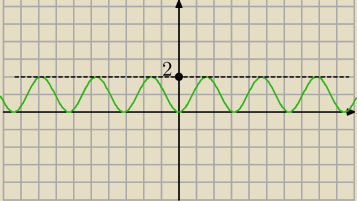
25 cze 08:27
bimbam: dzięki.
Źle spojrzałem na odpowiedź. Prawidłowa jest taka jak Tobie wyszła, czyli <0;2>
25 cze 19:51
bimbam: mam jeszcze pytanie.
Fakt, że tutaj jest kąt 2x, a nie "x" nie ma znaczenia

Kiedy by miało?
25 cze 19:57
Mila:
Gdyby było : f(x) = 2cos(x)
Zw=<−2,2>
25 cze 20:03
bimbam: aha, czyli amplituda.
dzięki
25 cze 20:06
bimbam: a jeśli mam taki przykład
y=sinIxI to robię tak samo jak y=f(IxI), czyli wykres z prawej strony OY przerysowuję na lewą
stronę OY,bo nie wiem ja to zrobić algebraicznie
25 cze 20:16
J:
rusujesz y = sinx , dla ujemnych odbijasz wykres symetrycznie względem osi OX
25 cze 20:37
J:
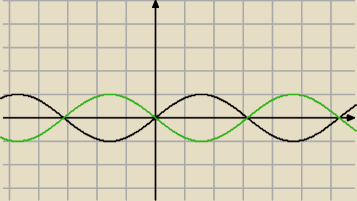
dla x≥ 0 − czarny wyktres: y = sinx
dla x <0 − zielony wykres: y = sin(−x) = − sinx
ten sam efekt uzyskasz odbijając y = sinx wzgledem osi OY
26 cze 08:27


 Kiedy by miało?
Kiedy by miało?
 dla x≥ 0 − czarny wyktres: y = sinx
dla x <0 − zielony wykres: y = sin(−x) = − sinx
ten sam efekt uzyskasz odbijając y = sinx wzgledem osi OY
dla x≥ 0 − czarny wyktres: y = sinx
dla x <0 − zielony wykres: y = sin(−x) = − sinx
ten sam efekt uzyskasz odbijając y = sinx wzgledem osi OY