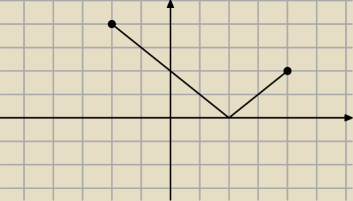
Funkcje jessica69: Na rysunku wykres f(x) Jakie współrzędne będą miały punkty wykresu g(x), jeśli g(x) = f(x − 3) ?

J: przesuń wykres o wektor v = [3,0]

Janek191: → w = [ 3 , 0 ]

jessica69: Przesuwam, ale w odpowiedziach jest, że te punkty mają współrzędne: lewy − [1, 4] prawy − [7, 2] a nie: lewy − [−5, 4] prawy − [1, 2]

jessica69: Czy to kolejny błąd w odpowiedziach, czy jakimś sposobem (x − 3) ewoluuje w (x + 3) ?

J: jest dobrze w odpowiedziach: x' = −2 + 3 = 1 oraz x' = 4 + 3 = 7 ( y się nie zmieniają )

Janek191: ( − 2, 4) + [ 3 , 0 ] = ( 1, 4) ( 4 , 2) = [ 3, 0 ] = ( 7 , 2) Jest ok

Janek191: W II wierszu miało być ( 4, 2) + [ 3, 0 ] = ( 4 + 3, 2 + 0) = ( 7, 2)

jessica69: f(x) → v[a,b] = f(x−a) + b Jeśli przesuwam o x[a,b] to odejmuję a, a nie dodaję ... Przepraszam, że męczę o takie elementarne rzeczy, ale miesza mi się już ta teoria...

jessica69: * o v[a,b]

Janek191: P = ( x , y) → w = [ a , b ] to P ' = ( x , y) + [ a , b] = ( x + a, y + b) x' = x + a y' = y + b

J: co innego jest zmiana formuły funkcji z f(x) na f(x−a) + b a co innego przesunięcie wykresu ... po prostu nowy wykres ma równanie y = f(x − a) + b, po przesunięcie o a w prawo i o b do góry