Pole figury Real: Oblicz pole figury ograniczonej liniami o równaniach: 4y=8x+x³ 4y=x+6

J: zrób szkic i ustal granice całkowania

Real: No właśnie mam problem z ustaleniem granic...

J: rozwiąż równanie: 8x + x³ = x + 6

Real: To wiem, tylko mam duże luki w wiedzy. x³+7x−6=0 i dla jakiego x W(x)=0 ?

Mariusz: (u+v)³+7(u+v)−6=0

	7
u3+v3−6+3(u+v)(uv+		)=0
	3

u³+v³−6=0

	7
uv+		=0
	3

u³+v³=6

	7
uv=−
	3

u³+v³=6

	343
u3v3=−
	27

	343
t2−6t−		=0
	27

	586*27
(t−3)2−
	729

	√15822		√15822
(t−3−		)(t−3+		)=0
	27		27

	81+√15822		81−√15822
(t−		)(t−		)=0
	27		27

	1
x1=		((81+√15822)(1/3)+(81−√15822)(1/3))
	3

600*27=16200 14*27=378 15822 243−343

J: ja raczej podejrzewam ,że było w zadaniu: 4y = 8x + x²

Real: Niestety jest tak jak napisałem. Gdyby było x² to by nie było problemu. Dzięki za pomoc

Mariusz: Ta inaczej prosta przetnie wykres wielomianu tylko w jednym punkcie Gdyby wielomian miał trzy pierwiastki rzeczywiste to można by policzyć sumę całek

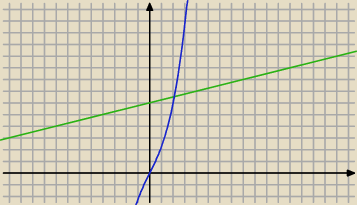
Mila: Nie ma obszaru ograniczonego przez te dwie krzywe.