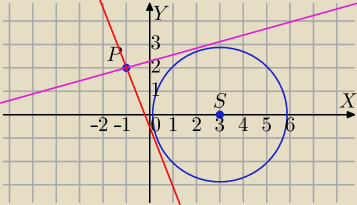
geometria analityczna-równanie okręgu zagubiony: Wyznacz równania stycznych do okręgu o równaniu (x−3)² + y² = 9 przechodzących przez punkt P (−1,2).

Benny: prosta y=ax+b ma być styczna i przechodzić przez punkt P więc 2=−a+b b=2+a y=ax+2+a Promień poprowadzony do stycznej jest odcinkiem prostopadłym do prostej, więc odległość od środka okręgu do prostej jest równa r=3 Nasza prosta w postaci ogólnej wygląda tak y−ax−2−a=0 S(3,0) (środek okręgu) mamy wzór na odległość punktu od prostej : d=U{|A*x_o + B*y₀ +C|}{√A²+B² d=3, A=−a, B=1, C=−a−2 x₀=3, y₀=0 Poradzisz sobie dalej?

Mila: y=ax+b równanie stycznej 2=−a+b b=2+a y=ax+2+a⇔ ax−y+2+a=0 odległość stycznej od środka okręgu S=(3,0) jest równa długości promienia r=3⇔

|a*3−0+2+a|
	=3⇔
√a2+1

|3a+2+a|=3√a²+1 /² (4a+2)²=9*(a²+1) 16a²+16a+4=9a²+9 7a²+16a−5=0 dokończ

zagubiony: Tak! Pięknie Wam dziękuję!

pigor: ...np. tak : (*) y−2=m(x+1) ⇔ mx−y+m+2=0 − równanie ogólne prostej przez dany punkt (−1,2), a ponieważ, ma być ona styczna do danego okręgu, a więc w odległości równej promieniowi od jego środka (3,0), czyli dla m spełniającego równanie :

	|3m−0y+m+2|
d=3 ⇔		= 3 ⇔ |3m+m+2|= 3√m2+1 ⇔
	√m2+1

⇔ |4m+2|= 3√m²+1 ⇔ (4m+2)²= 9(m²+1) ⇔ 16m²+16m+4= 9m²+9 ⇔ ⇔ 7m²+16m−5= 0 i √Δ= 2√99, więc m= ... lub m= ... masz dwie takie proste styczne (*) , oczywiście sprawdź moje rachunki za które nie dam głowy...

pigor: ..., no tak , jak zwykle marudziłem ..., mój spóźniony zapłon

zagubiony: Ale i tak dziękuję za chęci!