równanie płaszczyzny przechodzącej przez prostą i punkt cola: prosta l: x = 1+3t y = −1−t z = 2+t punkt P = (3,4,2) Proszę o pomoc..

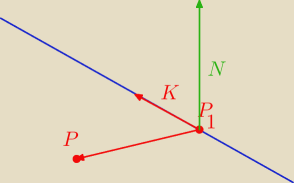
Godzio: Wektor kierunkowy prostej: K = [3,−1,1] Punkt z prostej: P₁(1,−1,2) oraz dany punkt P(3,4,2) dają nam wektor: PP₁ = [−2,−5,0] Wektor normalny prostej to iloczyn wektorowy wektorów rozpinających przestrzeń: N = K x PP₁ = [5,−2,−12] Równanie płaszczyzny przechodzącej przez P o wektorze normalnym N: 5(x − 3) − 2(y − 4) − 12z = 0 5x − 2y − 12z − 7 = 0 Mam nadzieję, że nie walnąłem się w obliczeniach

cola: mogłabym prosić o objaśnienie końcowego równania płaszczyzny? x−3 i y−4 rozumiem że wzięło się z punktu P, więc dlaczego nie ma nic przy z? dziękuję!

Godzio: Oczywiście powinno być, zdaje się, że na 'z' zajrzałem na wektor PP₁

cola: jeszcze jedno pytanie, czy przy liczeniu PP1 zawsze odejmujemy P od P1?

Godzio: Zależy czy liczysz PP₁ czy P₁P. W przypadku PP₁ to tak.