Zadanie z ciągu, funkcji i całka hela: Ciąg (−1)ⁿ , n∍N a. jest zbieżny b. nie jest ograniczony c. ma granicę nieskończoną d. zawiera podciąg zbieżny Funkcja ciągła a. ma granicę w każdym punkcie dziedziny b. jest różniczkowalna c. jest monotoniczna d. jest całkowalna Funkcja f o wzorze f(x)=x² a. ma maksimum lokalne w zerze b. ma minimum lokalne w zerze c. nie ma w ogóle ekstremów lokalnych d. ma ekstremum w punkcie różnym od zera e. jest wklęsła f. jest wypukła Przyrost wartości funkcji f jest całką a. funkcji f b. pierwszej pochodnej funkcji f c. drugiej pochodnej funkcji f Proszę o pomoc i krótkie objaśnienie dlaczego dana odpowiedź jest prawidłowa. dziękuję

5-latek: hela (−1)ⁿ n∊N nie jest ciagiem to tylko jakies wyrażenie Ciag ma swoje oznaczenie np. a_n = lub b_n= i td np. sprawdza) czy jest zbieżny a₁=−1 a₂=1 a₃=−1 a₄=1 i jaki wniosek ?

hela: Według moich notatek jest ciągiem... wydaje mi sie, że jest zbieżny, ale nie rozumiem tego zbyt...

J: Zapis (−1)ⁿ ... nie oznacza ciągu , ciąg a_n = (−1)ⁿ: a) nie jest zbieżny b) jest ograniczony c) nie ma granicy nieskończonej d) nie zawiera podciągu zbieżnego

J: 2) Funkcja ciągła: a) ma granicę w każdym punkcie dziedziny b) nie musi być różniczkowalna c) nie musi być monotoniczna d) jest całkowalna

5-latek: Otoz samo (−1)ⁿ nie jest ciagiem liczbowym Ciagiem liczbowym nazywamy kazda funkcje (zwróć uwagę na ten zwrot f: N→R okreslona na zbiorze N liczb naturalnych o wartościach w zbiorze R liczb rzeczywistych Jeśli ciag liczbowy to funkcja to czy funkcja jest np. x+3 czy powinien być zapis taki f(x)= x+3? Wiec w ciagach zamiast f(n) należy pisać (a_n) lub b_n lub c_n itd. dla n∊N Prawidlowy zapis powiniem wygladac np. nastepujaco a_n=(−1)ⁿ dla n∊N Dlaczego twierdzisz ze jest zbieżny ? Przeciez widzisz ze się rozbiega od −1 do 1

hela: jest ograniczony? skoro wychodzą tylko wartości 1 i −1?

J: tak ... z góry ogranicz go: M = 1 , z dołu: M = − 1

5-latek: tez bym powiedzil ze tak bo ciag a_n=(−1)ⁿ nie ma granicy

hela: czyli pierwsze to odpowiedz c? czy mam racje ze w trzecim pytaniu funkcja jest wypukla?

J: Cześć 5−latek nie rozumiem, co masz na myśli "też bym powiedział tak"

5-latek: Co do zadania nr 2 to jest takie twierdzenie Niech f: D→R będzie funkcja której dziedzina będzie niepusty podzbor D zbioru R Jeśli funkcja f jest rozniczkowalna (lewostronnie prawostronnie ) w punkcie x₀ ∊D to f jest funkcja ciagla (lewostronnie ,prawostronnie ) w punkcie x₀ . J czesc . Przyda się tutaj to twierdzenie ?

J: Jasne,że się przyda

5-latek: Witaj Pisalem to gdy jeszcze nie było Twojego postu . Odpowiedzialem na pytanie heli z 20:30 Jednak tez trafiłem

hela: Ok, ja rezygnuje... bo i tak nic z tego nie rozumiem, chociaż jedno już sie rozjaśniło dzięki

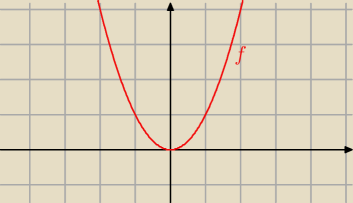
Janek191: f(x) = x² b) Ma minimum lokalne w zerze f ) Jest wypukła

b.: > (−1)ⁿ n∊N nie jest ciagiem to tylko jakies wyrażenie > Prawidlowy zapis powiniem wygladac np. nastepujaco an=(−1)ⁿ dla n∊N Skoro już się tak czepiamy, to Twój zapis − pomijając dodatkowe słowo 'dla' − nie jest lepszy od oryginalnego. Równość oznacza, że dwa obiekty są takie same, więc (−1)ⁿ jest tak samo dobre − albo tak samo złe − jak a_n = (−1)ⁿ. Typowo ciąg oznacza się tak: ((−1)ⁿ), albo ((−1)ⁿ)_n, albo ((−1)ⁿ)_n∊N, albo ((−1)ⁿ)_n=1^∞ − zależnie od tego, czy z kontekstu jest jasne, co jest argumentem i jaki zbiór przebiega. Można by też napisać (ale nie jest to tak typowe): ciąg a, gdzie a_n = (−1)ⁿ. > czy funkcja jest np. x+3 czy powinien być zapis taki f(x)= x+3? Znowu − nie ma znaczenia Formalnie funkcją jest f, więc zapis powinien być taki: funkcja f:X−>Y, gdzie f(x)=x+3. Albo taki jak w 3. zadaniu powyżej. Oczywiście poza ultrapurystami nikt się takimi drobiazgami nie przejmuje

henrys: nareszcie

b.: A co do samego zadania: 1 tylko d (wbrew temu, co wyżej napisane), w 2, d − raczej nie, np. funkcja f(x)=1/x jest ciągła, ale nie jest całkowalna. 4 − b: zachodzi f(b)−f(a) = ∫_a^b f'(x) dx (np. jeśli f jest ciągła na [a,b] oraz różniczkowalna na (a,b)).

5-latek: Dzien dobry b Definicje ciągu oraz jak oznaczamy ciag zaczerpnalem z książki Granica i ciaglosc funkcji Antoni Chronowski, Henryk Kąkol, Zbigniew Powazka z serii Matematyka dla ciekawych PIsza oni także: Ciag liczbowy określa się zwykle za pomocą wzoru ogolnego lub za pomocą wzoru indukcyjnego (rekurencyjnego ). \Dla przykładu ciag

	1
an=		jest określony wzorem ogolnym
	n

natomiast ciag \ a₁=1,a_n+1= √a_n+2 jest określony wzorem indukcyjnym . Ty pewnie masz wyksztalcenie nauczycielskie wiec weisz lepiej ode mnie (ja skonczylem stara szkole srednia i może zapisy się zmienily teraz Przyjmuje to do wiadomości Natomiast co do funkcji to zawszse piszse funkcja f(x)= lub y=. lub g(x)= Pozdrawiam

b.: Ja się czepiałem tylko dlatego, że Ty się czepiałeś Z oznaczeniami jest trochę tak, że trzeba znaleźć złoty środek, nie mam nic przeciwko zapisowi

	1		1
,,ciąg an=		'', jednak nie uważam go za lepszy niż ,,ciąg		'', tylko za dokładnie
	n		n

taki sam Oba są moim zdaniem odrobinę nieprecyzyjne (w zasadzie a_n jest n−tym wyrazem ciągu, czyli liczbą, a nie ciągiem), ale gdyby chcieć pisać wszystko tak, żeby było formalnie poprawne, to byłoby to mało zrozumiałe. No i poza tym wiele rzeczy niektórzy określają tak, inni siak. Na potrzeby szkolne zwykle ustala się definicje i oznaczenia (np. N={0,1,...}), ale w niektórych książkach mogą być inne (np. N={1,2,...}). Dlatego to że w jakiejś książce jest jakoś, to nie znaczy, że jak ktoś napisze inaczej to jest od razu źle.

5-latek: OK A napisz dlaczego w zadaniu nr 1 odpowiedz prawidlowa to d)

Janek191: a_n = (−1)ⁿ , n ∊ ℕ⁺ −1,1,−1,1,−1,1, ... Podciągi zbieżne: 1) 1,1,1,1,1, ... 2) − 1,−1,−1,− 1, ...

5-latek: Czesc henrys Co nareszcie ?

henrys: Co do ciągu (−1)ⁿ zgadzam się z b. Zdziwiło mnie, że nikt na to wcześniej nie zwrócił uwagi,a nie chciałem się wtrącać. Podobnie funkcję, również możesz inaczej zapisać niż wyżej, lub opisać słownie.