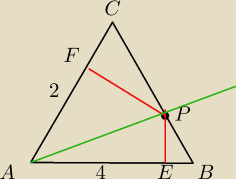
F. Michcio: Planimetria − dwusieczne, nie wychodzi wynik z odpowiedzią W ΔABC dane są długości boków AB=4, AC=2. Punkt P ∊ BC a jego odległość od każdego z boków AB i

	√15
AC wynosi		. Oblicz długość boku BC.
	4

Robię to tak: Punkt P jest jednakowo odległy od boków AC i AB czyli punkt P należy do dwusiecznej kąta BAC. Oznaczmy AE = x , EB = 4−x , AF = y , FC = 2−y Dodatkowo niech AP = d

	√15
Z treści zadania wiemy że FP = PE =
	4

ΔAEP ≡ ΔPFA (bbb) Z Pitagorasa wynika trzeci bok taki sam czyli x=y. a zatem EB=4−x i FC=2−x, AF=AE=x.

	AB		PB
Z twierdzenia o dwusiecznej wynika że stosunek		=
	AC		PC

Gdy PC=t to PB=2t Na koniec układam układ równań

	15
t2 = (2−x)2 +
	16

	15
4t2 = (4−x)2 +
	16

Mnożę peirwsze przez cztery i mam równanie

	60		15
4(2−x)2 +		= (4−x)2 +
	16		16

	45
Po rozwiązaniu równania 3x2 − 8x +
	16

dochodzę że BC=t+2t = 3t = √31 A niestety odpowiedź wychodzi 3.

pigor: ..., niech |∡BAC|=α , to pole ΔABC : ¹₂*2*4sinα= ¹₂*2*¹₄√15+¹₂*4*¹₄√15 ⇔ ⇔ 4sinα= ³₄√15 ⇔ sinα= ³₁₆√15 ⇒ cos²α=1−¹_16²*9*15 ⇔ ⇔ cos²α= (¹¹₁₆)² ⇒ cosα= ¹¹₁₆ i α−ostry, zatem BC²= 2²+4²−2*2*4cosα ⇔ BC²= 20−11 ⇒ |BC|=3 . ..

Michcio: Nie było w tym zbiorze trygonometrii przed tym zadaniem Najlepiej jak ktoś znajdzie błąd u mnie Gwarantuję że w obliczeniach u mnie błędu nie ma (tam gdzie są równania itd). Chodzi o sposób który jest o dziwo błędny

Michcio: Chociaż twoje rozwiązanie mi się podoba pigor

Kacper: W twoim rozwiązaniu dostajemy dwa wyniki:

	9
t=1, x=
	4

lub

	√31		5
t=		, x=
	3		12

I teraz trzeba się zastanowić, czy oba rozwiązania mają sens? Chwilka muszę się zastanowić, bo coś mi nie pasuje Będę w szkole, to powiem co i jak.

Michcio: No x=2,25 trochę nie bardzo jak tam jeden bok ma 2−x czyli byłby na minusie

Qulka: bardzo..bo to może być rozwartokątny i dlatego pseudo na minusie bo powinno być 2+x

Michcio: No tak , probówaliśmy z Δ rozwartokątnym i coś nie bardzo szło to narysować, zrobić itd. No dobrze, ale jak wyjdzie ten bok BC=√31 to wówczas patrzyłem na każdy trójkąt (nierówność Δ) i każdy Δ prostokątny tak aby przeciwprostokątna była dłuższa od przyprostokątnych i niby się wszystko zgadzało

Kacper: o 12 wam wszystko wyjaśnię

Kacper: Trójkąt o bokach 2,3,4 jest trójkątem rozwartokątnym i spełnia warunki zadania

Qulka: narysować mi się udało bez problemu (ten kąt rozwarty jest na Twoim rysunku na górze i wtedy x−2) i 3t=3 dla x=5/12 to kąt rozwarty jest na dole i wtedy 3t=√31

Kacper: Trójkąt o bokach 2,4,√31 spełnia warunki zadania

Kacper: Jak ktoś nie wierzy to mogę wysłać rysunki Teraz muszę zerknąć na rozwiązanie pigora i zobaczyć dlaczego ma tylko jedną wersję Mam Pigor założył, że kąt BAC jest ostry, a może być rozwarty

Michcio: Cześć Kacper Kacper podeślesz na ELMEX13@o2.pl Czyli z moim rozwiązaniem √31 jest ok ? Jeszcze muszę ogarnąć Δ rozwartokątny jakoś jako drugi przypadek

Kacper: Ok tylko je stworze w programie

Kacper: Z dużej litery mail?

Michcio: nie no z małych tylko napisałem tak żebyś L nie pomylił z I

Michcio: DosZło W Geogebrze to robiłeś Polecasz jakieś programy poza w/w do wykonywania rysunków np wykresu funkcji , geometrii ?

Kacper: Cabri Geometrii do wykresów 3D Poza tym są fajne narzędzia do rysowania online