Dziedzina dwóch zmiennych. Grzesiek: Dziedzina dwóch zmiennych. Sporządź rysunek na płaszczyźnie.

	xy
√
	4−x2+y2

Mam narazie tyle, że: 1. x² −y² ≠ 4 (co ma dać wykres hiperboli, ale nie wiem od czego zacząć...) 2. x ≥ 0 i y ≥ 0 i 4−x²+y² ≥ 0 (licznik i mianownik większe od zera) lub (logicznie) 3. x ≤ 0 i y ≤ 0 i 4−x²+y² ≤ 0 (licznik i mianownik mniejsze od zera), Blokuje mnie tu jak narysować (i wczesniej rozwiązać) x² −y² ≠ 4. Proszę o pomoc.

pigor: ...,

	xy		xy
f(x,y)= √		i D={ (x,y):		≥0 } ⇒
	4−x2+y2		4−x2+y2

⇒ ( xy ≥0 i 4−x²+y² > 0 ) v ( xy ≤ 0 i 4−x²+y² < 0 ) ⇔ ⇔ (x ≥0 i y ≥0 i x²−y²< 2²) v (x≤ 0 i y≤ 0 i x²−y² >2²) ) ⇔ ⇔ (x ≥0 i y≥0 i ^x2₄ − ^y2₄<1)) v (x≤0 i y≤0 i ^x2₄ − ^y2₄>1)) i teraz już rysujesz : sumę mnogościową punktów wewnątrz elipsy równoosiowej a=b=2 w I−szej ćw. oraz punktów poza tą elipsą w III−ciej ćwiartce wraz z półosiami OX i OY.. ...

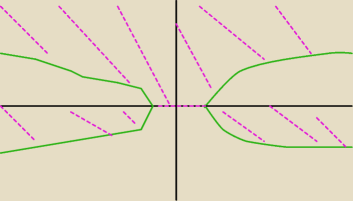
Grzesiek: Po przekształceniach widzę już ten wzór.

	x2		y2
Ale jedna rzecz. Nie upieram się, ale		−		=1 to bedzie wzór na hiperbolę,
	22		22

a nie elipsę, bo w elipsie jest suma, a nie różnica. Tak też wolphram sugeruje. Wyszedł mi taki rysunek. Dziedzina nie obejmuje wykresu paraboli,

	x2		y2
gdy		−		≥1 to na zewnątrz paraboli, dla x i y niezerowych,
	22		22

	x2		y2
oraz gdy		−		≤1 to wewnątrz paraboli, dla ujemnych x i y.
	22		22

pigor: ..., o kurde, no jasne że to hiperbola równoosiowa; przepraszam −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− więc tylko powiem tylko, że nie pisz o paraboli, tylko o krzywej − wykresie hiperboli no i nie wolno tu brać znaków nierówności słabych ≤, ≥, bo siedzi ona w mianowniku, tylko tak jaknapisałem w swoim poście x²−y² < 4 albo x²−y² > 4

Grzesiek: rzeczywiście masz rację, że nie może być znaku równości. Dzięki za pomoc. GZ