Pochodna 5-latek: Prosze o dokładne wyjaśnienie ; Niech f→R będzie funkcja której dziedzina jest niepusty podzbior D zbioru R liczb rzeczywistych Mowimy ze funkcja f jest rozniczkowalna w punkcie x₀∊D jeśli a) f jest funkcja okreslona w pewnym otoczeniu punktu x₀ i ma w tym punkcie pochodna skonczona

	f(x)−f(x0)
tutaj rozumiem ze f'(x0)= limx→x0		wiec ta granica nie jest rowna ∞
	x−x0

albo −∞ b) f jest funkcja okreslona w pewnym lewostronnym (prawostronnym ) otoczeniu punktu x₀ , ale nie jest okreslona w zadnym prawostronnym (leweo stronnym otoczeniu tego punktu i ma lewostronna (prawostronna ) pochodna skonczona w punkcie x₀ Ten podpunkt jest dla mnie bardzo zagwatmany

5-latek: Pewnie będę musial sobie przypomnieć co to jest otoczenie i sąsiedztwo ale na teraz prosiłbym

Draghan: Mnie uczyli, że pochodna f(x) w punkcie x₀ to granica:

	f(x0 + Δx) − f(x0)
f'(x0) = limΔx −> 0
	Δx

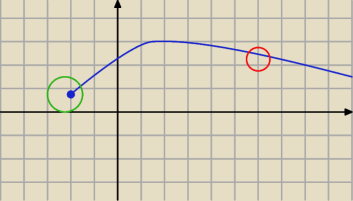
Mówiąc bardzo kolokwialnie (matematycy, proszę nie patrzeć ): Przypadek z podpunktu a tyczy się fragmentu funkcji gdzieś w środku przedziału. Przypadek z podpunktu b tyczy się krańca przedziału.

5-latek: OK Poczekam jeszcze na matematykow

5-latek: Obie te definicje sa równoczesne i rowne .

b.: W tej definicji żadamy 2 rzeczy: 1) żeby dziedzina była odpowiednio ,,duża'', konkretnie, żeby pewne otoczenie x₀ lub przynajmniej jednostronne otoczenie x₀ zawierało się w D, 2) żeby istniała granica ilorazów różnicowych, przy czym w przypadku, gdy pewne otoczenie x₀ zawiera się w dziedzinie, to bierzemy granicę obustronną, a w przeciwnym razie jednostronną Innymi słowy, bierzemy granicę obustronną, jeśli nam na to dziedzina pozwala, a jeśli nie pozwala (ale tylko wtedy), to jednostronną.

b.: (no i rzecz jasna ta granica musi być dodatkowo skończona)

5-latek: Dziekuje Ci bardzo za wyjaśnienie