całka bezendu: Polecenie to oblicz całkę podwójną

	x2
∬D		dydx x=1 y=x xy=4
	y2

D=1≤x≤2

	4
x≤y≤
	x

Sprawdzi ktoś ? http://zapodaj.net/8f61fc587b680.jpg.html

Draghan: Już słyszę głos mojej prowadzącej ćwiczenia. "Zero. Operuje pan funkcją, a dziedziny pan nie zbadał. Nie ma co sprawdzać".

ZKS:

	x3
−		+ x
	4

ZKS:

	9
Wynik to		.
	16

bezendu: Dzięki ZKS

Mila: Wynik:

9
16

bezendu: Kochani mogę Was jeszcze prosić o pomoc w kilku zadaniach ?

Mila: ZKS , jak błyskawica.

5-latek: Czesc Draghan Dawno Cie nie widziałem na forum Tak naprawdę to Pani prowadzaca podajac przepis na funkcje powinna okreslic dziedzine . Taki zapis np. f(x)= x+1 jest tylko zwykłym wyrażeniem bez podania dziedziny To ze zazwyczaj za dziedzine bierze się caly obszar okreslonosci czyli np. w tym f(x)=x+1 będzie zbior liczb R to wcale nie oznacza ze ja mogę sobie przyjąć np. D_f=<−23,87654303> . Zgodzisz się ze dziedzina tej funkcji jest tez ten przedzial . No ale już dalej nie wspominamy prowadzącej do dostanie czkawki

Hugo: takie banały całka podwójna, Hugo 4,0 egzamin z wielokrotnych

5-latek: W takim razie Bądź pochwalony Hugo

52: Hugo tym bardziej powinieneś pomóc

Hugo: Wykształcenie nie piwo nie musi być pełne bezendu

bezendu: ∬_D √x²+y²dydx D=x²+y²≤2x http://zapodaj.net/713acd27f47e1.jpg.html

bezendu: Hugo idź być fajny gdzieś indziej

ZKS: .

bezendu: Dzięki ZKS i przepraszam Cię bardzo za jakoś zdjęcia

ZKS: Dostanę skrzywienia kręgosłupa. Jakość zdjęcia okej tylko na następny raz obróć zdjęcie.

bezendu: Ok, mam taką całkę ∬_Dxy²dxdy ale obszar maskra 1≤x²+y²≤2 , y≥x≥0

ZKS: Pierścień.

52: Obszar mi taki wyszedł:

	π		π
U:		≤φ≤
	4		2

1≤r≤√2 pewnie źle ...

ZKS: Chodzi mi o 1 ≤ x² + y² ≤ 2. Dalej rozrysuj sobie 0 ≤ x ≤ y i zaznacz część wspólną.

Draghan: Witaj, 5−latek. Nie pokazywałem się, bo miałem mnóstwo innych zajęć, a z matematyką byłem w miarę na bieżąco... I masz całkowitą słuszność co do dziedziny. Ale niektórym nie przetłumaczysz. Jutrzejszy egzamin z matematyki będzie moim trzecim, a jestem pierwszy raz w ogóle dopuszczony do pierwszego terminu. I nie dlatego, że z matmy kuleję. Może najlepszy nie jestem, ale jednak coś tam umiem. Grupy które miały nieszczęście się dostać pod opiekę mojej prowadzącej, są w większej części niedopuszczone do egzaminu. Grupy z drugą prowadzącą są z kolei w większej części z egzaminu w ogóle zwolnione. Ja po prostu już się nauczyłem, że dla mojego dobra piszę wszędzie dziedzinę. A to tylko przykład. W równaniach różniczkowych pani profesor na wykładzie mówiła, żeby nie robić za wiele założeń i raczej nie uwzględniać rozwiązań trywialnych... A u nas na ćwiczeniach za to lecą punkty... Nie przetłumaczysz. Ale co ja tu będę się żalił. Mam nadzieję że jutro zdam i już nie będę musiał więcej kochanej pani oglądać.

J: Wycinek pierścienia

bezendu: ?

J:

ZKS: 52 .

bezendu:

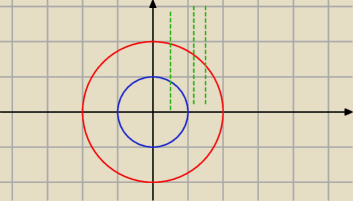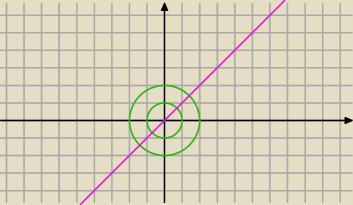
	π
własnie możecie powiedzieć czemu obszar U{π}[4}≤φ≤
	2

52:

	17√2−12
Moja odp. to
	60

pewnie coś skopałem...

J: bo punkty pierścienia leżą nad prostą y = x

bezendu: ok, dzięki.

ZKS: Jak sobie rozpiszesz bezendu to otrzymasz 0 ≤ x ≤ y 0 ≤ rcos(φ) ≤ rsin(φ)

	π		π
0 ≤ ctg(φ) ≤ 1 ⇒ 45o ≤ φ ≤ 90o ⇒		≤ φ ≤		.
	4		2

bezendu: Masz jeszcze czas na dwa zadanka ?

ZKS: 52 wynik jest okej.

52: Dzięki ZKS

ZKS: Wrzucaj beznedu jest dużo osób, które może Ci pomóc ja powoli się zawijam znowu uczyć się na egzamin.

bezendu: http://zapodaj.net/373a01a6a75f1.jpg.html ∬_D √ydxdy D: y=x² i y=1 wychodzi y ? co jest bez sensu

52: za y wstaw 1... ograniczenie z góry

J:

2		2
	√1 , a nie		√y
3		3

bezendu: i teraz wychodzi ok

Mila:

bezendu: Mila możesz jeszcze raz wytłumaczyć mi z tą całką niewłaściwą ?

Mila: Czego tam nie rozumiesz? Wracam do tamtego wpisu.

bezendu: Tej granicy.