Pochodna kierunkowa bezendu: Obliczyć pochodną kierunkową funkcji f(x, y) = x√x²+y⁴ w punkcie (x₀, y₀) = (1, −1)

	π
w kierunku wersora tworzącego kąt		z dodatnią częścią osi X
	4

tg45⁰=1 więc druga współrzędna tego 1 a jak ustalić pierwszą współrzędną ?

J:

	√2		√2
v = [		,		]
	2		2

bezendu: @J ale zanim policzę wektor kierunkowy muszę policzyć jego długość wektora i stąd moje pytanie pierwszą mogę wziąć dowolną ? bo druga to tg45⁰=1

J: wersor ma długość 1 , a do pochodnej kierunkowej potrzebujesz tylko jego wspórzędne

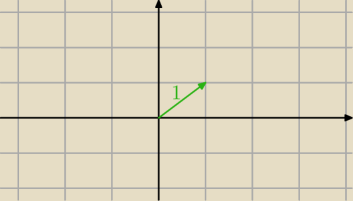
J: i policz jego współrzędne

bezendu: J http://blog.etrapez.pl/pochodne/pochodne-kierunkowe-znowu-cos-nowego/ zobacz ostatni punkt w tym linku

J: i wszystko się zgadza ... w tym co podałeś wektor ma długość √10 , a w tym zadaniu mamy długość 1 , zatem wektor kierunkowy taki, jak Ci podałem

J: akurat patrzyłem na pierwszy przypadek ... stąd √10

bezendu: czyli jak mam podany jakiś punkt i kąt α np (2,3) α=180 v[2,tg180⁰ ] tak ?

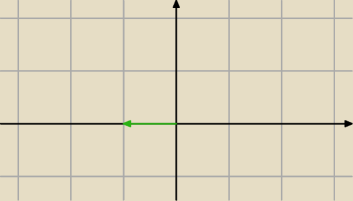
J: to jest Twój wektor kierunkowy: v = [ −1,0] ( bo jego długość to 1 ) wektor kierunkowy obliczasz ze wzoru:

	1
vk→ =		*v→
	IvI

bezendu: no ja wiem, że wekotr kierunkowy wyznaczam z tego wzoru, ale żeby to wyznaczyć muszę mieć długość |v| a do tego potrzebne mi sa współrzędne wektora. Zaraz wstawię rozwiązanie.

bezendu: Może ktoś sprawdzić rozwiązanie: http://zapodaj.net/de425f16c1e27.jpg.html

bezendu: up

J: pochodne dobrze .... obliczeń nie sprawdzałem

bezendu: Obliczenia, też Dziękuje bardzo. Mogę jeszcze Cię wykorzystać ?

J: dawaj ... nie ja , to ktoś inny

bezendu: Mam całkę podwójną

	x2
∬D		dxdy i obszary y=x x=1 xy=4
	y2

D=1≤x3

	4
		≤y≤x
	x

?

bezendu: Chodzi czy dobrze mam obszar

J: lepiej będzie odwrócić kolejność całkowania podziel y na dwa zkresy: 1 ≤ y ≤ 2 orz 2 ≤ y ≤ 4 i ospowiednio funkcje : x = f(y)

Qulka: x do 1 do 2

bezendu: 1≤x≤2 a nie mogę tak zostawić ?

J: możesz

bezendu: Obliczyć dwoma sposobam ∬_D √ydxdy obszar ograniczony y=x² y=1 −1≤x≤1 a y ? jeden sposób to całka iterwoana a drugi ?

J: x² ≤ y ≤ 1

bezendu: Ok, a wiesz jaki to jest drugi sposób policzenia tego bo jakoś nie mogę wpaść ?

J: zmiana kolejności całkowania : 0 ≤ y ≤ 1 0 ≤ x ≤ √y

bezendu: ok

J: tak policzymy połowę, czyli wynik razy 2 lub −√y ≤ x √y

bezendu: w tej pierwszej całce chyba ten drugi obszar całkowania to

	4
x≤y≤
	x

bo funkcja y=x ogranicza z dołu ?