... Phoebe Campbell: Proszę o sprawdzenie − ciągłość funkcji. 1) Wykaż, że funkcja f jest ciągła w punkcie X₀ = 2.

	⎧	6 − x2 dla x < 2
a) f(x) =	⎨
	⎩	x dla x ≥ 2

lim_x−>2⁻ (6 − x²) = 2 lim_x−>2⁺ = 2 lim_x−>2 f(x) = f(2)

	⎧	1x − 3 dla x < 2
b) f(x) =	⎨
	⎩	(x − 3)3 dla x ≥ 2

	1
limx−>2− (		) = −1
	x − 3

lim_x−>2⁺ (x − 3)³ = −1 lim_x−>2 f(x) = f(2) 2. Wykaż, że funkcja f nie jest ciągła w punkcie x₀ = 0.

	⎧	−x dla x ≤ 0
a) f(x) =	⎨
	⎩	x2 + 1 dla x > 0

lim_x−>0⁻ = 0 lim_x−>0⁺ = 1 Nie istnieje lim_x−>0 f(x)

	⎧	x2 − 1 dla x ≠ 0
b) f(x) =	⎨
	⎩	0 dla x = 0

Nie wiem jak to zrobić... wykazać, że −1≠0?

Saizou : a jaka jest def. ciągłości funkcji w punkcie

Saizou : i pytanie czy masz wykazać ciągłość czy zbadać ciągłość ?

Phoebe Campbell: W pierwszym wykazać, że funkcja jest ciągła w danym punkcie, a w drugim, że nie jest. Definicja jest taka, że musi istnieć granica obustronna dla danego punktu oraz, że musi być ona równa f(punkt). Problem mam bardziej z rachunkami.. nie wiem zapisać 2b.

Saizou : to nie jest definicja, to jest warunek konieczny i wystarczający żeby funkcja była ciągła w punkcie, a jak masz wykazać coś to masz korzystać z definicji.

Phoebe Campbell: W książce znalazłem taką definicje: Funkcję f:(a;b) −> R nazywamy ciągłą, jeżeli jest ciągła w każdym punkcie przedziału (a;b) Ale jak to zastosować do 2b? I czy pozostałe podpunkty zrobiłem dobrze?

Saizou : tu masz de. http://www.math.edu.pl/ciaglosc-funkcji

Saizou : wykazując nieistnienie ciągłości powołaj się na def. Heinego i weź dwa pociągi

Saizou : przepraszam, ale muszę teraz lecieć, bo się zasiedziałem, będę dopiero jutro i wtedy będę mógł Ci pomóc

Phoebe Campbell: Okej, dzięki za pomoc i materiały.

Phoebe Campbell: Temat nadal aktualny 1) Czy 1 zadanie jest ok? 2) Czy 2a jest zrobione dobrze w myśl def. Heinego, bo wykazałem, że granice jednostronne są różne, więc granica obustronna w tym punkcie nie istnieje to funkcja nie jest ciągła w tym punkcie. 3) nadal nie wiem jak zrobić 2b

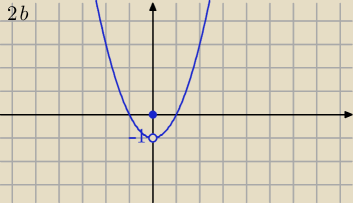
Mila: 1) a) f(2)=2 i granica jest równa 2⇔f(x) jest ciągła w x₀=2 1) b) g=−1 f(2)=−1 f(x) ciągła w x₀=2 2) a) dobrze. b) patrz wykres lim_x→0±f(x)=−1⇔lim_x→0 f(x)=−1 f(0)=0 granica w x₀ jest różna niż wartość f(0)⇔funkcja nie jest ciągła w x₀=0

Phoebe Campbell: Teraz rozumiem, dzięki Ci bardzo Mila

Mila: Masz proste funkcje, to rysuj wykresy, od razu widać czego się spodziewać.

Phoebe Campbell: Zapamiętam