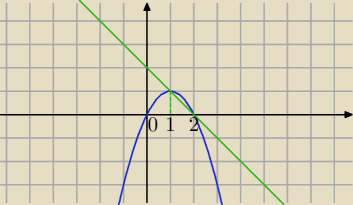
całka podwójna - blad Wtorek: Witam, mam problem z taką oto całką podwójna ∫∫ lnxdxdy , w obszarze D ograniczony krzywymi : y=−x²+2x , y=−x+2 Po narysowaniu wykresu mam do oblicznia całke z 2 −x²+2x ∫∫ lnxdxdy= ∫ { ∫ lnxdy} dx=... D 1 −x+2 Liczę całke nieoznaczoną: Następnie ∫lnxdy= lnx∫dy= ylnx+C −x²+2x [ylnx]I = −x²lnx+3xlnx−2lnx −x+2 ∫( −x²lnx+3xlnx−2lnx)dx = po obliczeniu kazdej calki wyszedl wynik = −¹₃x³lnx+¹₉x³+³₂x²lnx−³₄x²−2xlnx+2x+C Jednak po podstawieniu granic calkowania, wynik wychodzi inny niz w kalkulatorze, gdzie robie blad? co jest zle?

Przemysław:

	2		19
−		ln2+
	3		36

Czy to jest podobne do wyniku, jaki ma być?

Wtorek: Tak , wychodzi tak samo.

Wtorek: To gdzie jest blad?

Przemysław: Za chwilkę napiszę jak mam, tylko chwilę, plx

Przemysław: ∫²₁∫^−x2+2x_−x+2lnxdydx= ∫²₁lnx(−x²+3x−2)dx= <teraz przez części>

	x3		3x2		x3		3x2		1
((−		+		−2x)lnx)21−∫12((−		+		−2x)*		dx=
	3		2		3		2		x

	x3		3x2		x2		3x
((−		+		−2x)lnx)21−∫12(−		+		−2)dx=
	3		2		3		2

	23		3*22		x3		3x2
((−		+		−2*2)ln2)−(−		+		−2x)21=
	3		2		9		4

	2		8		12		1		3
−		ln2−(−		+		−4)+(−		+		−2)=
	3		9		4		9		4

−2		19
	ln2+
3		36

Przemysław: Czyli, że błąd masz dopiero tam, gdzie liczysz te wszystkie całki, na końcu, ew. przy wstawianiu granic całkowania.

Mila: ₁∫²[_−x+2∫^−x2+2x(lnx)dy]dx=₁∫²[ylnx]_−x+2^−x2+2x= =₁∫²(lnx*[−x²+2x+x−2]dx= =₁∫²(−x²lnx+3xlnx−2lnx)dx=

	1		1		3		3
=[		x3−		x3lnx+		x2lnx−		x2+2x−2xlnx]12=
	9		3		2		4

	8		8		3		1		3
=		−		ln(2)+		*4ln(2)−3+4−4ln(2)−		+0−0+		−2+0=
	9		3		2		9		4

	7		1		8		19		2
=		−		+2ln(2)−		ln(2)=		−		ln(2)
	9		4		3		36		3

Wtorek: dziękuje wam juz mam dobrzę , błędy tkwią w szczegółach , trzeba ostroznie liczyc.

Mila: