Okręgi Michcio: W okręgu o promieniu 5 poprowadzono cięciwy AB i CD długości 6. Wykaż że cieciwa AC = 9,6 cm.

Kacper:

Metis:

pigor: ..., treść twoja, czy oryginalna, bo na pierwszy rzut oka nie jest jednoznaczna − czy czegoś nie ominąłeś −np. o tych cięciwach, bo wszystkich przypadków nie chce mi się rozpatrywać ...

Michcio: BC = 6 OJEJ PRZEPRASZAM Zrobiłem to metodą deltoidu który powstaje ale dumny z tego rozwiązania nie jestem !

Bogdan: Ciekaw jestem tej metody deltoidu, pokaż to rozwiązanie

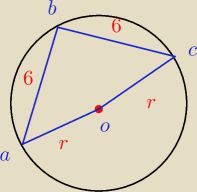
Michcio: Powstał deltoid o bokach 6,5,5,6. Liczę jego pole na dwa sposoby

1
	*AC*BO (iloczyn przekątnych)=2,5AC
2

Z drugiej strony dzielę deltoid na dwa trójkąty równoramienne ABO i BOC (5,5,6) których pole da się łatwo policzyć Wynik wychodzi ale rozwiązanie dziwne.

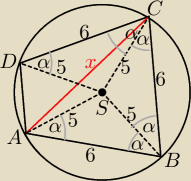
Bogdan: Szkic rozwiązania (trzeba jeszcze podać założenia).

	62 + 52 − 52
Z twierdzenia cosinusów w trójkącie BCS i ABS: cosα =		= 0,6
	2*6*5

cos2α = 2cos²α − 1 = 2*0,36² − 1 = −0,28 Z jedynki trygonometrycznej: sin2α = √1 − (−0,28)² = 0,96

	x		x
Z twierdzenia sinusów w trójkącie ABC:		= 2R ⇒		= 2*5 ⇒ x = 9,6
	sin2α		0,96

Michcio: Dobrze a to moje rozwiązanie jak oceniasz

Bogdan: Twoje rozwiązanie jest dobre i jest proste, podoba mi się . Spróbuj poszukać jeszcze prostsze rozwiazanie

Bogdan: cos2α = −0,28 Od razu, bez tw. sinusów, ale z tw. cosinusów w trójkącie ABC: x² = 6² + 6² + 2*6*6*0,28 = 92,16 ⇒ x = 9,6

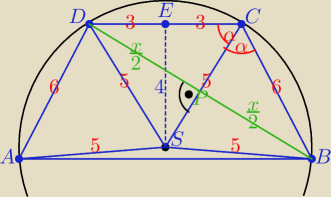
Bogdan: ΔCES: |ES| = √25 − 9 = 4 i sinα = 0,8

	x
ΔPBC:		= 6*sinα ⇒ x = 12*0,8 = 9,6
	2

pigor: ..., albo, jeśli O−środek okręgu, D− punkt wspólny AC z BO⊥AC i dla uproszczenia zapisu |AC|=2|AD|=2x=?, a |OD|=y, to x²+(5−y)²=6² i (*) x²+y²=5² /− stronami ⇒ ⇒ (5−y)²−y²=36−25 ⇔ 25−10y=11 ⇔ y=1,4 , stąd i z (*) x²=5²−1,4² ⇔ x²=23.04 ⇒ x=4,8 ⇒ 2x=|AC|=9,6. c.n.w. ... :