 Podpowiedź.
g(x)=x2−3x−4 jest różniczkowalna w R
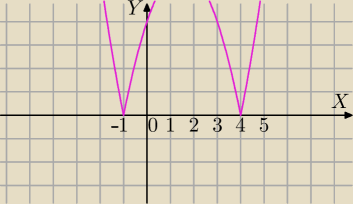
f(x)=|x2−3x−4| może nie być różniczkowalna w punktach zmiany wzoru;
Oblicz miejsca zerowe g(x)
f(x)=x2−3x−4 ⇔x2−3x−4≥0 ⇔x≤−1 lub x≥4
f(x)=−(x2−3x−4) ⇔x2−3x−4<0 czyli ?
Badasz pochodną w x=−1 i x=4
Podpowiedź.
g(x)=x2−3x−4 jest różniczkowalna w R
f(x)=|x2−3x−4| może nie być różniczkowalna w punktach zmiany wzoru;
Oblicz miejsca zerowe g(x)
f(x)=x2−3x−4 ⇔x2−3x−4≥0 ⇔x≤−1 lub x≥4
f(x)=−(x2−3x−4) ⇔x2−3x−4<0 czyli ?
Badasz pochodną w x=−1 i x=4