| x2 | ||
y = | ||
| x2−9 |
| x2 | ||
f(x) = | , x ≠ − 3 i x ≠ 3 | |
| x2 − 9 |
| 2x*( x2 − 9) − x2*2x | − 18 x | |||
f '(x) = | = | = 0 ⇔ x = 0 | ||
| ( x2 − 9)2 | (x2 − 9)2 |
| 2x*(x2−9)−2x*x2 | ||
f'(x)= | ||
| (x2−9)2 |
| 2x3−18x−2x3 | ||
f'(x)= | ||
| (x2−9)2 |
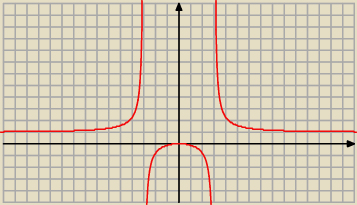 Dla x < 0 i x ≠ − 3 jest f '(x) > 0
Dla x = 0 jest f '(x) = 0
Dla x > 0 i x ≠ 3 jest f '( x) < 0
więc funkcja f osiąga w x0 = 0 maksimum lokalne równe f( 0) = 0
W ( −∞ , −3) , ( − 3, 0) funkcja f rośnie
W ( 0, 3 ) , ( 3 , +∞ ) funkcja f maleje
Dla x < 0 i x ≠ − 3 jest f '(x) > 0
Dla x = 0 jest f '(x) = 0
Dla x > 0 i x ≠ 3 jest f '( x) < 0
więc funkcja f osiąga w x0 = 0 maksimum lokalne równe f( 0) = 0
W ( −∞ , −3) , ( − 3, 0) funkcja f rośnie
W ( 0, 3 ) , ( 3 , +∞ ) funkcja f maleje
