;) marcin1c: f(x)=^−4x_x²+1 Oblicz wartosć min i max w przedziale <0;4>

Janek191:

	− 4 x
f(x) =		< 0 ; 4>
	x2 + 1

	− 4*(x2 + 1) − ( −4 x)*2 x		4*( x2 − 1)
f '(x) =		=		= 0 ⇔
	(x2 + 1)2		(x2 + 1)2

⇔ x = − 1 lub x = 1 Niech x ∊ < 0; 4> Dla x < 1 jest f '(x) < 0 , a dla x > 1 jest f '(x) > 0 więc funkcja f w punkcie x_o = 1 osiąga minimum lokalne równe f( 1) = − 2 Obliczam jeszcze:

	− 16
f( 0) = 0 i f(4) =
	17

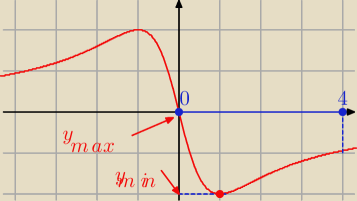
Odp. y_min = f(1) = − 2 , y_max = f(0) = 0 =================================== Patrz też na wykres