TALES Michcio: Na jednym z boków ΔABC obrano punkt P i poprowadzono przez niego proste równoległe do pozostałych boków. Podzielimy one Δ na dwa trójkąty o polach P₁ i P₂ i równoległobok. Wyznacz pole ΔABC w zależności od P₁ i P₂

henrys:

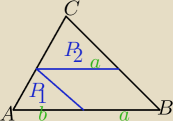
P1		b2
	=		P−pole trójkąta ABC
P		(a+b)2

P2		a2
	=
P		(a+b)2

P2		a2
	=
P1		b2

	bh1		2P1
P1=		⇒ h1=
	2		b

	ah2
P2=
	2

	a		P2
Pole równoległoboku = ah1 = 2P1		=2P1√
	b		P1

	P2
PΔ=P+P2+2P1√
	P1

Janek191: W ostatnim wierszu jest błąd ?

henrys: Tak brakuje indeksu dolnego

henrys: Powinno być P₁+ P₂+...

henrys: Jeszcze można uprościć: P_Δ=P₁+P₂+2√P₁P₂

Janek191: Teraz jest ładny wzorek

Kacper: