Oblicz pole czworokąta AEDC Wojtas: Ze środka przyprostokątnej BC trójkąta prostokątnego ABC poprowadzono odcinek DE prostopadły do przeciwprostokątnej. Wykaż że trójkąt ABC i DBE są podobne, a następnie oblicz pole czworokąta AEDC, jeśli IBSI=8cm, IACI=6cm Prosze o pomoc kompletnie tego nie rozumiem

J: chyba źle przepisałeś/aś treść

Wojtas: błąd jest IBCI=8cm reszta jest dobrze 3x sprawdzałem

Wojtas: nikt nie wie jak to zrobic

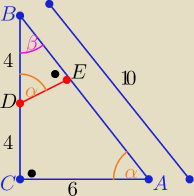
Eta: ΔABC∼ ΔDEB z cechy (kkk) Z tw. Pitagorasa w Δ ABC : |AB|= √36+64= 10 Z podobieństwa trójkątów ABC i DEB :

|DE|		4		|BE|		8
	=		⇒ |DE|=2,4 i		=		⇒ |DE|=3,2
6		10		4		10

	8*6		2,4*3,2
P(AEDC)= P(ABC) − P(DEB) =		−		= ........
	2		2

Wojtas: dziękuje bardzo

Eta: Na zdrowie dorzucam ...

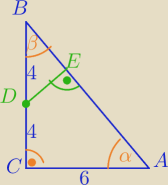
Mila: ΔDEB−Δprostokątny , ma jeden kąt ostry równy kątowi B w ΔABC⇔ trójkąty są podobne cecha kkk. |AB|=10

	4		2
ΔDEB∼ΔABC w skali k=		=		⇔
	10		5

PΔDEB		2
	={		)2⇔
PΔABC		5

	4
PΔDEB=		*PΔABC
	25

	1
PΔABC=		*6*8=24
	2

	4		96
PΔDEB=		*24=		=3.84
	25		25

P_AEDC=24−3.84 Albo tak:

DB		AB
	=
DE		AC

4		10
	=
DE		6

|DE|=2,4 Z tw. Pitagorasa obliczasz |EB| i potem pole trójkąta DEB.