CA
hs:
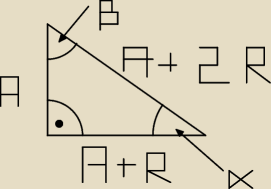
Długości boków trójkąta prostokątnego tworzą ciąg arytmetyczny. Oblicz tangens jednego z kątów
ostrych trójkąta.
16 cze 22:01
kyrtap: najpierw wylicz wartość a korzystając z tw. Pitagorasa oraz własności ciągu arytmetycznego
16 cze 22:09
Eta:
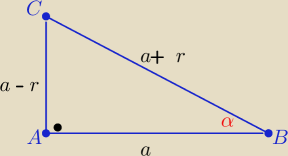
a>0 , r<a
z tw. Pitagorasa:
(a−r)
2+a
2=(a+r)
2 ⇒ a
2−4ar=0 ⇒ a(a−4r)=0 ⇒ a= 4r
| | 3r | | 3 | | 4 | |
|AC|= 3r , |AB|=4r , to tgα= |
| = |
| , tgβ= |
| |
| | 4r | | 4 | | 3 | |
16 cze 22:11
hs: Znaczy zrobiłem coś takiego :
a
2+(a+r)
2=(a+2r)
2
a
2+a
2+2ar+r
2=a
2+4ar+4r
2
a
2−2ar−3r
2=0
Δ
a=16r
2
Ale nie wiem czy to ma jakikolwiek sens, dlatego tego nie pisałem
16 cze 22:13
hs: Dziękuję Eta
16 cze 22:13
Eta:
Mogłeś dokończyć ...
√Δ=4r >0
| | 2r+4r | |
a= |
| = 3r v a= −r <0 odrzucamy |
| | 2 | |
itd...
16 cze 22:17
kyrtap: koleżanka wyżej dobrze radzi
16 cze 22:24
Eta:
16 cze 22:25