ciągi monotonicznosc łobuziacek : Moglby mi ktos rozwiazac? Opanowalam juz obliczanie miejsc sume i sprawdzanie ciagu geo i aeytmetycznego ale monotonicznosc wciaz nie an= 5/n+1 ( / = kreska ułamkowa ) bn= −3/n

Piotr: https://matematykaszkolna.pl/strona/1704.html

Eta:

	5		5		5		5		5
an :		,		,		,		,		,....... malejący
	2		3		4		5		6

	3		3
bn : −3, −1,5; −1, −		, −		,..... rosnący
	4		5

łobuziacek : Niestety nic z tego nie ogarniam

łobuziacek : Ale rozpisal by to ktos z dobrym sercem? Mam zagrozenie

Eta:

	5		5
a1=		=
	1+1		2

	5		5
a2=		=
	2+1		3

itd......... podobnie

	−3
b1=		= −3
	1

	−3
b2=		= −1,5
	2

itd.........

Piotr: mozna tak sprawdzac monotonicznosc ciagu ? ja bym sprawdzil a_n+1 − a_n

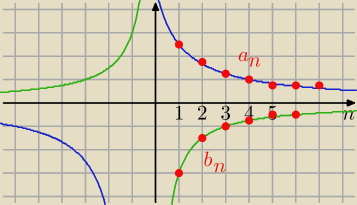
Eta: W tych przykładach : a_n : licznik dodatni, mianownik co raz mniejszy i też dodatni ⇒ ciąg malejący b_n : licznik ujemny , mianownik coraz większy i dodatni ⇒ ciąg rosnący lub tak ( z wykresu) dla n∊N+

PW: Dla ciągów o wyrazach dodatnich często zgrabniej jest zastosować spostrzeżenie: a_k+1 < a_k ⇔ U{a_k+1{a_k} < 1, czyli zamiast badać różnicę − bada się iloraz. W tym zadaniu

	ak+1		5   k+2		k+1
		=		=		< 1.
	ak		5   k+1		k+2

Pokazaliśmy, że dla dowolnej naturalnej k prawdziwa jest nierówność

	ak+1
		< 1,
	ak

czyli a_k+1 < a_k, która oznacza że ciąg jest malejący.

łobuziacek : Dziekuje bardzo !

Piotr: czyli odpowiedzi sie nie doczekalem. a tu tak pokazuje to Gustlik https://matematykaszkolna.pl/forum/forum.py?komentarzdo=1378

PW: Standardowo bada się różnicę, bo taka jest definicja: Ciąg (a_n) jest malejący, gdy dla dowolnej naturalnej k a_k+1 − a_k < 0. Gustlik przesadza tłumacząc łatwiejsze pojęcie monotoniczności ciągu za pomocą trudniejszego pojęcia monotoniczności funkcji.