Monotoniczność Tysek: Zbadaj monotoniczność i znajdź ekstrema funkcji f(x)=x³−2[x]

john2: Średnio pomogę, ale zainteresował mnie ten przykład. Wydaje mi się, że będzie tak: ([x])' = 0 dla x niecałkowitych dla x całkowitych pochodna nie jest zdefiniowana. Więc dla x niecałkowitych prawdą powinno być coś takiego: f'(x) = 3x² − 2 * 0 f'(x) = 3x² 3x² > 0 jest zawsze spełnione, więc funkcja rośnie dla wszystkich x niecałkowitych. Wydawałoby się, że nie ma ekstremów skoro pochodna nie zmienia znaku, ale patrząc na wygenerowany wykres: http://www.mathe-fa.de/en#result wpisz sobie wzór: x³ − 2 * floor(x) i patrząc na definicję ekstremów, wygląda na to, że mamy minimum lokalne dla każdego x całkowitego, ale nie wiem, jak do tego dojść samemu. Ktoś, mam nadzieję, się wypowie.

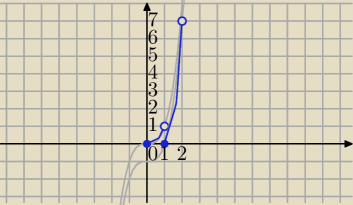
Mila: y=x³ funkcja rosnąca Rozważmy wykres przedziałami. 1) x∊<0,1) [x]=0 f(x)=x³−0=x³ funkcja rosnąca (niebieskie wykresy) min lokalne dla x=0 f_min=0 2) x∊<1,2) [x]=1 f(x)=x³−1 funkcja rosnąca f_min=0 3) x∊<2,3) [x]=2 f(2)=8−2=6 wartość najmniejsza w tym przedziale Dalej podobnie dla x>0 Rozważaj podobnie w przedziałach dla x<0. funkcja jest rosnąca przedziałami.

john2: Ciekawe rozwiązanie. Dzięki Mila. Jeden mały chochlik w 2): f_min = −1

john2: i w 3) wzór funkcji to f(x) = x³ − 2[x]

Mila: Tak , nie zauważyłam tej dwójki, trzeba poprawić. Rozumowanie zostaje.