Zbadaj czy funkcja ∫ jest ciągła w punkcie x_0 Napoleon: Funkcja ∫ określona jest wzorem ∫ (x) = x+4 gdy −4 <X ≤ 0 x²=2x+5 gdy 0 <x <2 3x, gdy x≥ 2 a) zbadaj czy funkcja ∫ jest ciągła w punkcie x₀ = 0 b) oblicz granice jednostronne funkcji w punkcie x₀ = 2 Kochani, serdeczna prośba, czy ktoś byłby dla tyle uczynny i mógłby pomóc mi z tym zadaniem? Nie mam zielonego pojęcia od czego nawet zacząć, a bardzo mi zależy żeby to rozwiązać.

Janek191: Funkcję oznaczamy zazwyczaj literką f Symbol ∫ oznacza całkę

Napoleon: Mój błąd. Podobno to nie jest trudne zadanie, ale nie mam pojęcia co z nim zrobić Pomóżcie dobrzy ludzie

Janek191: Popraw w II wierszu Tam pewnie powinien być + ?

Napoleon: f (x) = x+4 gdy −4 2=2x+5 gdy 0 <x <2 3x, gdy x≥ 2

Napoleon: http://screenshootereu.blob.core.windows.net/engine4files/psepnagucmuieexldgkqpwvjweoudnbjvybtzzmatkejwhidklezbbwtwusimlrolkngcdmdujxesmnpwkkrjbiubixehenhtpyl tutaj jest zdjęcie zadania, bo jaki błąd wkradł się w liczby jakie napisałem f(x) = x+4 gdy −4 <X ≤ 0 x²=2x+5 gdy 0 <x <2 3x, gdy x≥ 2

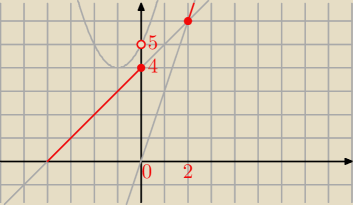
Janek191: a) f(0) = 4 + 0 = 4 oraz lim (x² + 2 x + 5) = 5 x→0⁺ więc funkcja f nie jest ciągła w x_o = 0

Napoleon: dzięki wielkie, jesteś moim mistrzem!

Janek191: b) x₀ = 2 lim f(x) = 2² +2*2 + 5 = 13 x → 2⁻ oraz lim f(x) = 3*2 = 6 = f(2) x→ 2⁺

Napoleon: http://screenshootereu.blob.core.windows.net/engine4files/ydkseiwtkwykbngvosrciujtoolqltbtemhkbmlxkejzajvpbaqrwsddureqxghrvegpgvubgureljsetvoldjxlidqkivaewrev Może wiedziałbyś jeszcze, jak wyliczyć wartości granic? Z tego co wywnioskowałem, dziedzina wynosi tutaj (−4,1); (1,1); (3,4)(6,2), ale nie wiem czy dobrze kombinuje

Janek191: x→2⁻ czytamy: x dąży do 2 z lewej strony ( czyli przez liczby < 2) x→ 2⁺ czytamy: x dąży do 2 z prawej strony ( czyli przez liczby > 2 )

Janek191: a) Df = ( − 6, 6 > b) 1. lim f(x) = 2 x→ − 4⁻ 2. lim f(x) = 4 x→ 3⁻ 3. lim f(x) = 2 x→ 0 c) Trzy punkty nieciągłości :

Napoleon: http://screenshootereu.blob.core.windows.net/engine4files/djkvlyyzoedloxjhtgicvurrzoinvwgkistvfpqfjhrdbqeyfoehrwyjsswwplesytdvenbdpcsodnqjkkigrysltkcntuqydyfi Dzięki wielkie stary, ratujesz mi życie! Jakbyś zerknąć na to ostatnie zadanie, byłbym dozgonnie wdzięczny I daj znać gdzie Ci piwo wysłać

Janek191: Słabo widać

	x2 + 6 x + 9
f(x) =		?
	x2 + x − 6

lim f(x) = lim f(x) ? x→− 3⁻ x → − 3⁺

Napoleon: tak

Janek191:

	( x + 3)2		x + 3
f(x) =		=
	( x + 3)*( x −2)		x − 2

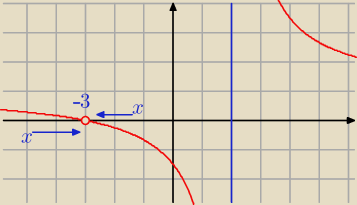
Janek191: Dziedzina f : x ≠ − 3 i x ≠ 2

	− 3 + 3		0−
lim f(x) =		=		= 0
	− 3 −2		− 5

x→ −3⁻

	− 3 + 3		0+
lim f(x) =		=		= 0
	− 3 − 2		− 5

x→ −3⁺

Napoleon: Dzięki wielkie mistrzu!