Pole powierzchni ograniczonej krzywymi
Paweł: Oblicz pole powierzchni ograniczonej krzywymi y=x2−x i y=x
16 cze 17:58
henrys: 2−∫12 x2−xdx−∫01x2−xdx
16 cze 18:18
Marcin:
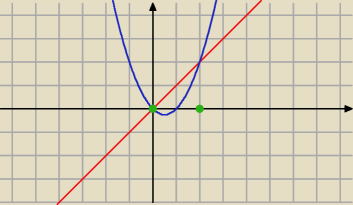
Całka od 0 do 2 ∫(x−x
2−x)dx = całka od 0 do 2 ∫−x
2dx
| | 1 | | 1 | | 8 | |
−[ |
| x3]od zera do dwóch −(0− |
| *8)= |
| |
| | 3 | | 3 | | 3 | |
16 cze 18:32
Marcin: | | 8 | |
Poprawiam się. Wynik to, oczywiście − |
| |
| | 3 | |
16 cze 18:36
henrys: to nie prawda pole trójkąta jest równe 2 więc pole tej figury nie może być większe od 2
16 cze 18:37
henrys: jeszcze lepiej pole ujemne?
16 cze 18:37
16 cze 18:38
Marcin: Poprawiam się.
| | 4 | |
Całka od 0 do 2 ∫(2x−x2)dx = |
| Mój błąd |
| | 3 | |
16 cze 18:45
Mila:
x
2−x=x⇔
x
2−2x=0
x*(x−2)=0
x=0 lub x=2
| | 1 | |
0∫2(x−(x2−x))dx=0∫2(−x2+2x)dx=[− |
| x3+x2]02= |
| | 3 | |
16 cze 18:45
henrys: 
16 cze 18:48