rozwiąż równanie Asmander: co robie źle cos2x − 5sinx −4 =0 1 − sin²x −sin²x −5sinx −4 =0 −2sin²x −5sinx −3 =0 t = sinx t∊<−1,1> 2t² +5t +3 =0 Δ=25 − 24 = 1

	−5−1		−3
t1 =		=		∊ nie należy <−1,1>
	2		2

t₂ = −1 sinx=−1

	π
x=−		+ 2kπ
	2

52: złe t₁ oraz t₂

Asmander: ale źle jest to obliczone sprawdzałem drugi raz i nic nie widze

Asmander:

	−5−1		3
t1 =		=−6/4=−
	4		2

	−5+1
t2 =		=−1
	4

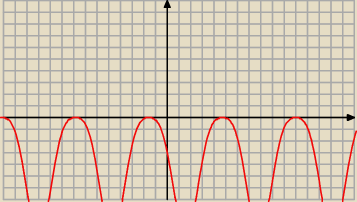Janek191: 1 − 2 sin² x − 5 sin x − 4 = 0 2 sin² x + 5 sin x + 3 = 0 2 t² + 5 t + 3 = 0 Δ = 25 − 24 = 1

	− 5 − 1
t =		= − 1,5
	4

	− 5 + 1
t =		= 1
	4

sin x = − 1

	π
x = −		+ 2π*k , k − dowolna liczba całkowita
	2

================

Asmander: dziękuję

Janek191: Powinno być: t = − 1

Janek191:

	− b − √Δ
x1 =
	2 a

	− b + √Δ
x2 =
	2 a