parametr Asmander:

	1
( sinx +		)(sinx +2k)=0
	2

wyznacz wartości parametru dla których równanie ma cztery różne rozwiązania w przedziale <−π,π>

J: skoro pierwszy nawias ma dwa różne pierwiastki , to drugi musi mieć również dwa

	1		1
pierwiastki, ale różne od x= −		oraz x =		,
	2		2

to ma miejsce gdy: sinx + 2k = 0 ⇔ sinx = − 2k

	1		1
i − 1 , −2k < 1 i −2k ≠		i −2k ≠ −
	2		2

Asmander: dzięki

J:

	1
nie tak ... : − 1 < −2k < 1 i −2k ≠ −
	2

Asmander:

	1
czyli sinx=−
	2

	π
sinx=−
	6

	π		7π
x=−		+ 2kπ v x=		2kπ
	6		6

J: Ty masz w rozwiązaniu tylko podać wartość parametru k ... musi on jednocześnie spełniać obydwa warunki z postu: 14:07

Asmander: −1 < −2k < 1

1		1		1
	>k>−		−2k≠
2		2		2

	1		1
k∊(−		,		)
	2		2

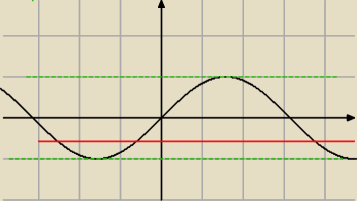
J: zielona prosta y = −2k , może zająć dowolne położenie pmiędzy y = 1 i y = −1,

	1
oprócz czerwonej : y = −
	2

J: nie .... − 1 < −2k < 1 ⇔ 2 > k > − 2 , czyli: k ∊ (−2,−1/2) U (−1/2,2)

Asmander: Czyli muszę wykluczyć te dwa pierwiastki

−π		7π		−5π
	i −		−2π =
6		6		6

ZKS: Dla k = 0 mamy trzy rozwiązania.

J: upss ... Twoje rozwiązanie jest dobre

J: Racja ZKS ... chyba zmęczenie ... wyrzuć z rozwiązań k = 0

Asmander: o źle przepisałem przykłąd powinno być (cosx +2k) =0

J: Masz już zamęt... rozwiązanie: k ∊ (−1/2,0) U (0,1/2)

Asmander:

	1
(sinx+		)(cosx +2k) =0
	2

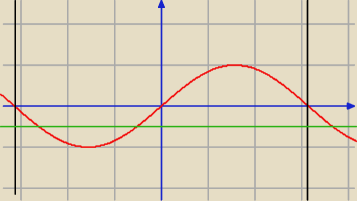
ZKS: Ładnie pokazałeś z rysunkiem, a z niego wszystko idzie odczytać.

	1
Z rysunku odczytujemy, że prosta y = −2k nie może być prostą y = 0 ∧ y = −		oraz
	2

musi należeć do przedziału −1 < −2k < 1.

J: .. tylko przeoczyłem y = 0

ZKS:

	1		1		1
Zatem odpowiedź to k ∊ (−		;		) \ {−		; 0}
	2		2		4