Równanie 2 stopnia z parametrem Michcio: Ustal ile punktów wspólnych może mieć parabola o ramionach skierowanych do góry i wierzchołku w punkcie (0,−4) z okręgiem o równaniu x²+y²=16 Rozpatruję układ równań y=ax²−4 oraz x²+y²=16 Podstawiam pierwszy y do drugiego równania i dochodzę do postaci x²(a²*x²−8a+1)=0 ⇔ x=0 lub a²x²−8a+1=0 Nie wiem co to jest to x=0 ale chyba nic konkretnego a²x²−8a+1=0 a² * x² = 8a−1

	8a−1
a ≠ 0 (właściwie to a>0) czyli x2=
	a2

No i kompletnie nie wiem co dalej...

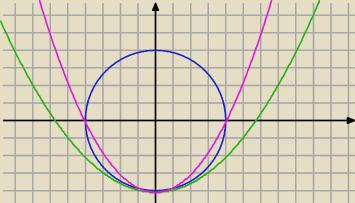
Qulka: dla a≤1/8jedno rozwiązanie dla a>1/8 trzy rozwiązania

ZKS:

	y + 4
y = ax2 − 4 ⇒ x2 =		∧ a > 0
	a

x² + y² = 16

y + 4
	+ y2 = 16
a

y² + y + 4 − 16a = 0 Δ = 1 − 4 * (4 − 16a) = 64a − 15

ZKS: Oczywiście, że muszę coś zjeść o tej porze. ay² + y + 4 − 16a = 0 Δ = 1 − 4 * a(4 − 16a) = 64a² − 16a + 1 = (8a − 1)²

Piotr: smacznego

ZKS: A dziękować.

Michcio: Zks jest chyba ok 👌 ale u cb wyjdą 2rozw i jedno. A u qulki wyszło jedno i trzy

ZKS: Jest chyba ok, a co jest źle? Jeżeli nie widzisz nic to ja zapiszę w ten sposób, może to zauważysz. ay² + y + 4 − 16a = 0 a(y² − 16) + y + 4 = 0

	4a − 1
(y + 4)(ay − 4a + 1) = 0 ⇒ y = −4 ∨ y =		.
	a

	4a − 1		1
Teraz jeżeli		= −4 ⇒ a =
	a		8

	−4 + 4
otrzymamy jedno rozwiązanie y = −4, stąd x2 =		⇒ x2 = 0 ⇒ x = 0.
	1   8

Mamy, więc jedno rozwiązanie x = 0 ∧ y = 0,

	1
jeżeli teraz 0 < a ≠		to mamy rozwiązanie
	8

	4a − 1		4a − 1   + 4 a
y =		∧ x2 =		,
	a		a

	4a − 1   + a a
rozpatrujemy rozwiązanie x2 =		, jeżeli prawa strona jest ujemna
	a

dostaniemy sprzeczność.

4a − 1   + 4 a
	< 0
a

8a − 1		1		1
	< 0 ∧ 0 < a ≠		⇒ a ∊ (0 ;		)
a2		8		8

Natomiast jeżeli prawa strona będzie nieujemna otrzymamy rozwiązania

8a − 1		1		1
	≥ 0 ∧ 0 < a ≠		⇒ a ∊ (		; ∞)
a2		8		8

	1
Dla licznika 8a − 1 = 0 otrzymamy x = 0 jedno rozwiązanie, ale już wcześniej dla a =
	8

	1
mieliśmy jedno rozwiązanie, więc dla a ∊ (		; ∞) mamy dwa rozwiązania w sumie trzy.
	8

	1
Podsumowując dla a ∊ (0 ;		] mamy jedno rozwiązanie
	8

y = −4 ∧ x = 0,

	1
dla a ∊ (		; ∞) otrzymamy trzy rozwiązania
	8

	4a − 1		√8a − 1
(y = −4 ∧ x = 0) ∨ (y =		∧ x = ±		.
	a		a