Funkcja wykładnicza + parametr łup łup: Zbadaj liczbę rozwiązań równania w zależności od wartości parametru m (m ∊ R): |2 − (¹₃)^x| = m² − 1 W odpowiedziach jest: Równanie nie ma rozwiązań dla m ∊ (−1, 1); ma 1 rozwiązanie dla m ∊ (−∞, −√3) ∪ {−1, 1} ∪ <√3, +∞), dwa rozwiązania dla m ∊ (−√3, −1) ∪ (1, √3) Narysowałam ten wykres i tylko część odpowiedzi mi się pokrywa − nigdzie nie wychodzi mi √3 ani −√3 − nie wiem skąd się to w ogóle bierze. Mógłby mi ktoś pomóc z tym zadaniem? Byłabym wdzięczna

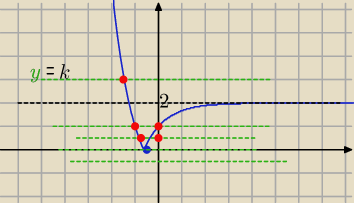
Eta: y=k , k= m²−1 0 rozwiązań dla k <0 ⇒ m²−1<0 ⇒ m∊(−1,1) 1 rozwiązanie dla k=0 lub k>2 ⇒ m²−1=0 lub m²−1>2 ⇒ m =± 1 lub m²−3>0 ⇒ m∊(−∞. −√3) U ( √3, ∞). 2 rozwiązania dla 0< k <2 ⇒ ..... dokończ

łup łup: No tak, zapomniałam o asymptocie... Dziękuję bardzo za pomoc