Zadanie poprawkowe - proszę o pomoc!
Doris: Jutro zadanie poprawkowe, jedno z wielu, brzmi ono tak:
W trapezie równoramiennym, którego kąt ostry ma 45 stopni, suma długości wysokości i dłuższej
podstawy jest równa 12. Jaki długości powinny mieć boki trapezu aby jego pole było największe?
15 cze 23:00
Doris: Mam problem bo w ogóle nie wiem jak się do tego zabrać...
15 cze 23:09
Ja: Ekstremum funkcji kwadratowej
15 cze 23:16
Eta:
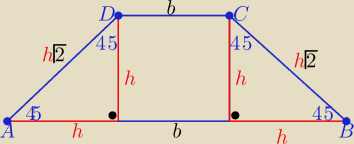
3h+b=12 ⇒ b= 12−3h , h∊( 0,4)
| | 2b+2h | |
P= |
| *h = (b+h)*h= (12−2h)*h = −2h2+12h |
| | 2 | |
| | −12 | |
hmax= |
| = 3 to b= 12−9= 3 |
| | −4 | |
to |AB|= .... , |DC|=.... , |AD|=|BC|= ....
15 cze 23:24
Doris: A nie przypadkiem:
2h + b = 12 ⇒ b = 12 − 2h ?
15 cze 23:31
Eta:
Suma wysokości i dłuższej podstawy =12
h+a=12 ⇒ h+ 2h+b=12
15 cze 23:32
Doris: Już nic
15 cze 23:33
Eta:
Co "nic" ?
15 cze 23:33
Doris: Rozkminiam rozkminiam i się trochę gubię, ale próbuję cały czas...
15 cze 23:35
Eta:
To jeszcze dorzucam ......
15 cze 23:36
Doris: Teraz już rozumiem na tyle:
3h+b=12 ⇒ suma długości wysokości i dłuższej podstawy OK!
max h może być 4 min to 0 (tak?)
Pole, pole... a+b/2*h czyli no właśnie. bierzemy krótszą podstawę plus dłuższą przez dwa i
mnożymy razy wyskość, ale tego tu u góry nie rozumiem jeszcze.
15 cze 23:38
Eta:
P(h)= −2h
2+12h −−− parabola ramionami do dołu
| | −b | |
funkcja osiąga max dla odciętej wierzchołka hw= |
| = |
| | 2a | |
czy teraz jasne?
15 cze 23:48
Doris: Ch... chyba tak.
16 cze 00:02