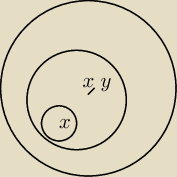
definicja pary uporządkowanej john2: Definicja pary uporządkowanej − może ktoś w języku prymitywnym mi ją wytłumaczyć? Czytam i czytam i nie rozumiem tego zapisu: (x,y) = { {x}, {x,y} } Rozumiem istotę, tzn. że najpierw ma być x potem y, ale jak zwizualizować ten zbiór po prawej stronie? Widzę, że jest to zbiór z dwoma podzbiorami. Jeden ma jeden element x, drugi dwa elementy x i y. Domyślam się, że {x} zawiera się w {x,y} i wychodzi mi taki rysunek, który nie wiem, jak się ma do kolejności elementów x i y.

nieuczciwy: Ja to widzę tak, że x to najmniejszy z podzbiorów, a y to {x,y}/{x}

john2: Zgoda, ale jak ma się to do kolejności elementów x i y? W jaki sposób zbiór { {x}, {x,y} } obrazuje, że x jest tym pierwszym elementem, czy też współrzędną, a y drugim?

nieuczciwy: Zbiór składa się z 2 elementów − zbioru jednoelementowego − to jest x pierwszy element pary i zbioru dwuelementowego. Jeśli od drugiego zbioru (dwuelementowego) odejmiemy zbiór pierwszy (jednoelementowy) to zostanie y (czyli drugi w kolejności element pary Drugi zbiór nie jest zapisany jako po prostu {y} bo wtedy nie było by wiadomo co jest pierwsze w parze x czy y. Stąd ta sztuczka z różna ilości elementów.

john2: Czyli rozumiem, że w zapisie { {x}, {x,y} } zbiór {x} jest pierwszy, a {x,y} drugi? Czyli zbiór { {x}, {x,y} } nie jest równy zbiorowi { {x,y}, {x} } ?

john2: Chyba jednak nie zrozumiałem, bo wiadomo, że {a,b} = {b,a}, więc dalej nie wiem, z czego wynika to, że na pierwszym miejscu jest x, a na drugim jest y.

nieuczciwy: Zbiór { {x}, {x,y} } jest równy zbiorowi { {x,y}, {x} }. I właśnie dlatego że mamy jeden zbiór jednoelementowy a drugi dwuelementowy wiemy jaki będzie "porządek" w parze. Czyli nie ważne jak zapiszemy ten zbiór w uporzadkowanej parze zawsze na pierwszym miejscu będzie element ze zbioru jednoelementowego a na drugim róznica zbioru 2−elementowego i 1−elementowego

john2: Czyli, jeśli dobrze rozumiem: Zapis { {x}, {x,y} } oznacza parę uporządkowaną (x,y), gdzie pierwszy jest x, ponieważ x jest elementem zbioru jednoelementowego, a potem jest y, ponieważ jest elementem zbioru dwuelementowego, gdzie jest też x, ale jego nie powtarzamy. Czyli po prostu obowiązuje jakaś zasada, że najpierw się bierze pod uwagę zbiór 1−elementowy, potem 2−elementowy, potem 3−elementowy...? Mam wrażenie, że umyka mi jakaś niezwykle oczywista oczywistość.

nieuczciwy: No tak mi się wydaje: Zapis {{a} {g,a}} oznacza parę (a,g) A zapis {{z}, {g,z}} oznacza parę (z,g)

john2: Ok. Dziękuję bardzo.