Własności i granice ciągów szerzawiak: Zad 1 Oblicz granicę

	x2 − 8x + 15
a) lim
	x2 − 9

x→3 Tu daję link do zdjęcia zadań bo trochę za dużo pisania : http://zapodaj.net/ddac3d67a55ea.jpg.html To czy zdam jest zależne od Was z góry dziękuję i proszę o rozwiązanie

Janek191: Np. na wzór

	( x − 3)*( x − 5)		x − 5
f(x) =		=
	( x − 3)*( x + 3)		x + 3

więc

	3 − 5		2		1
lim f(x) =		= −		= −
	3 + 3		6		3

x→3

J: Nie pisz głupot ... to czy zdasz , czy nie ... zależy wyłącznie od Ciebie , a ściślej od tego, co do tej pory zrobiłeś, aby sie tego nauczyć

szerzawiak: Masz rację w 100 % Mimo to prosiłbym o rozwiązanie

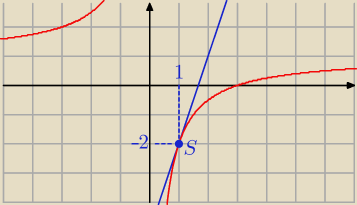
Janek191: z.3

	x − 3
f(x) =		, x ≠ 0
	x

	1 − 3
xo = 1 więc yo = f(xo) = f(1) =		= − 2
	1

Punkt styczności S = ( 1, − 2) Prosta styczna ma równanie y = a x + b gdzie a = f '( x_o)

	3		3
f '(x) = ( 1 −		) ' =
	x		x2

więc

	3
a =		= 3
	12

y = 3 x + b oraz S = ( 1 , − 2), więc − 2 = 3*1 + b b = − 5 Odp. y = 3 x − 5 ============= Patrz też na wykres:

J: Zad 3 i 4 ... potrafisz policzyć pochodną ?

J: dobra .... już nie licz pochodnych

szerzawiak: Szacnek dla takich ludzi jak Ty którzy pomagają innym

J: Niestety ...Janek191 tylko Ci szkodzi.

szerzawiak: Zaliczałem inne działy i ten mi został miałem tylko dzień żeby ogarnąć ten cały dział ... Dasz rade zrobić 2 i 4 zadanie ? i w pierwszym 2 przykłady ?

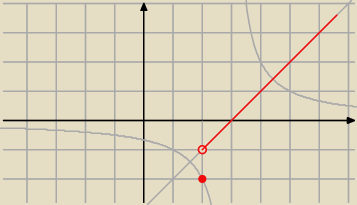
Janek191: z.2

	2
f(x) =		dla x ≤ 2
	x − 3

= x − 3 dla x > 2

	2		2
f( 2) =		=		= − 2
	2 − 3		−1

a lim f(x) = − 1 x → 2⁺ więc funkcja f nie jest ciągła w punkcie x_o = 2

J: Pomogę ... gotowca nie dostaniesz ... 4) Ile wynosi pochodna funkcji ?

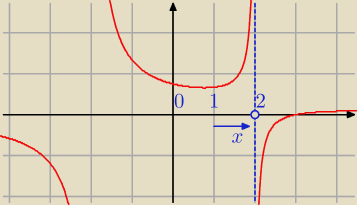
Janek191: z.1 c)

	x −3		x − 3
f(x) =		=
	x2 − 4		( x − 2)*( x + 2)

więc

	2 − 3
lim f(x) =		= +∞
	0−

x→ 2⁻ x→ 2⁻ czytamy x dąży do 2 z lewej strony Patrz też na wykres .

Janek191: z.1

	2   9 +   x
d) f(x0 = 9 x2 + 2 x}{ 3 x2 − 1} =
	1   3 −   x2

więc

	9 + 0
lim f(x) =		= 3
	3 − 0

x→+∞

Janek191: Miało być

	9 x2 + 2 x
f(x) =		= ... ( dzielimy licznik i mianownik przez x2 )
	3 x2 − 1