kombinatoryka zadania , pilne peper: 1.Rzucamy kolejno 5 razy monetą. Ile jest wszystkich takich wyników w których za drugim razem wypadł orzeł. 2.Z urny zawierającej 7 ponumerowanych kul losujemy kolejno tworząc 4 cyfrową liczbę ile jest możliwości wylosowanie liczby większej od 5555 3.Z talii 52 kart losujemy 2 karty. Ile jest możliwości wylosowania: a) 2 pików b) co najmniej jednego asa c) dwóch takich samych figur 4.Rzucamy 3 razy kostką. Ile jest wszystkich możliwych wyników w których za ostanim razem wypadło 1lub 6. 5.Wśród 7 książek dwie są mniejszego formatu ile jest wszystkich ustawień książek takich , aby wszystkie książki tego samego formatu stały obok siebie 6.W urnie znajduje się 5 kul białych i 4 czarne. Losujemy kolejno 2 kule (bez zwracania) Ile jest możliwości wylosowania a) za pierwszym razem kuli czarnej b) kul tego samego koloru c) za drugim razem kuli białej Proszę o pomoc, który wzór gdzie zastosować i jak?

peper: może mi ktoś pomóć ?

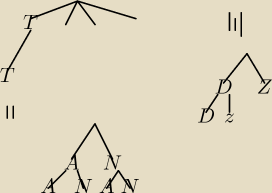
Silwest: No to pierwsze z dzrzewka To chyba tak bedzie ze najpierw rzucamy 1 raz moze nam wypasc reszka lub orzel i ponizje drugi raz tez reszka lub orzel gdzie T to reszka a N to orzel Czyli jest 2 mozliwosci mozemy najpierw rzucic Reszke pozniej orła lub za 1 razem orla i za 2 rowniez Co do reszty zaraz zrobie ;> jak mi sie bedzie chcialo

Silwest: 2 nie wiem raczej bo troszke go ni rozumiem nie mamy podanych numerow n o ale moze kots inny zrobi

	13
3 jezeli sie nie myle to wszystkich pikow jest 13 czyli P(T)=		gdzie T to piki i znowu
	52

drzewo No nie chce mi sie bawic ale jest 4 kolory a my mamy wylosowac 2 piki czyli tyle drzewa wystarczy

	13		12
Szansa na to ze wylosujemy najpierw pika to		a za 2 razem		czyli
	52		51

13		12
	*		= oblicz sobie
52		51

asy

	4
P(A)=
	52

i znowu drzewo 2 Czyli

4		3		4		38		38		4
	*		+		*		+		*		= Oblicz sobie ;>
52		51		52		51		52		51

3 o ile dobrze pamietam jest po 4 karty tej samej figury czyli

	4
P(D)=
	52

i znowu drzewo czyli

4		3
	*		= oblicz
52		51

chyba dobrze ;>