parametry
Asmander: Wyznacz te wartości parametru m∊R, dla których równanie
| m−1 | |
| x2 −2(m+2)x + m+4 = 0 nie ma rozwiązań |
| m−5 | |
| | m−1 | |
nie ma rozwiazań czyli Δ<0 i |
| >0 tak  |
| | m−5 | |
14 cze 18:58
ZKS:
| | m − 1 | |
Wytłumacz dlaczego |
| > 0? |
| | m − 5 | |
14 cze 19:08
Asmander: bo powstanie nam funkcja liniowa

14 cze 19:13
Metis: ≠0
14 cze 19:14
ZKS:
To ciekawe, a poza tym to funkcja liniowa nie ma rozwiązań?
14 cze 19:14
Asmander: będzie drugi przypadek i musimy w nim zbadać czy on również nam nie da rozwiązania powstanie
−2(m+2)x + m+4 = 0
14 cze 19:17
ZKS:
Możesz jakoś się obronić przed tą funkcją linową, bo może nie mieć rozwiązań, ale kiedy?
14 cze 19:18
Metis: Ja oczywiście uogólniam.
Ale rozpatrujemy parametry m dla, których :
| | m−1 | | m−1 | |
1) Równanie kwadratowe |
| x2−2(m+2)x+m+4=0 nie ma rozwiązań , wtedy |
| ≠0 |
| | m−5 | | m−5 | |
| | m−1 | |
2) Równanie liniowe −2(m+2)x+m+4=0 nie ma rozwiązań dla |
| =0 |
| | m−5 | |
14 cze 19:19
ZKS:
Sam się uczysz, czy chodzisz do szkoły?
Jak otrzymałeś to −2(m + 2)x + m + 4 = 0?
14 cze 19:20
Asmander: funkcja liniiowa nie ma rozwiązań ⇔ gdy a=0 i b≠0
14 cze 19:21
ZKS:
| | m − 1 | |
Dla |
| = 0 równanie przyjmie postać |
| | m − 5 | |
−2(1 + 2)x + 1 + 4 = 0.
14 cze 19:22
ZKS:
To się obroniłeś.

Tutaj zachodzi nam takie coś?
14 cze 19:22
Metis: Racja
ZKS skopiowałem z postu wyżej nie sprawdzając

Przepraszam ze się wciąłem ale nie widziałem, że piszesz.
14 cze 19:23
Asmander: a = −6 nie spełnia ono 1 warunku.. a=0
14 cze 19:24
Asmander: to moge liczyć, czy coś jest źle dalej?
14 cze 19:25
ZKS:
Pisz, pisz nawet lepiej to ja będę mógł jak coś zerkać tylko.

14 cze 19:29
ZKS:
| | m − 1 | |
To zapisz sobie, że dla |
| mamy rozwiązanie, więc nie uwzględniamy go przy |
| | m − 5 | |
końcowym rozwiązaniu.
14 cze 19:30
ZKS:
| | m − 1 | |
Oczywiście dla |
| równego 0. |
| | m − 5 | |
14 cze 19:31
Asmander: Δ<0
m≠1
| | m−1 | |
Δ=(m+2)2 − 4 * |
| * (m+4) < 0 |
| | m−5 | |
| | m2 +3m − 4 | |
Δ=m2 + 4m + 4 − 4* |
| < 0 |
| | m−5 | |
czy dobrze to rozwiązuje?
14 cze 19:34
Asmander: aha chyba już wiem co robie źle, nie zauważyłem [−2(m+2)]2
14 cze 19:47
Asmander: dobra nie wiem jak rozwiązać Δ wychodzi mi 4m
3 −24m
2 −60m −64 <0
| | 4m2 +12m −16 | |
4m2 +16m +16 − |
| < 0 |
| | m−5 | |
a dobrze chociaż dotąd rozwiązałem

14 cze 19:54
Metis: b= [−2(m+2)]2
m≠1 ⋀ m≠5 − nie dzielimy przez 0.
14 cze 19:55
Asmander: Δ = [−2(m+2)] −4 * (m+4) < 0
Δ = 4m2 +16m +16 −4m −16 <0
Δ = 4m2 +12m < 0
4m(m +3) < 0
m ∊ (−3 ,0)
14 cze 19:59
Metis: Źle.
| | 4m2−20 m+16 | |
4m2 +16m +16−[ |
| ]<0 |
| | m−5 | |
14 cze 19:59
Asmander: W odpowiedziach wyszło :
| | 3−√73 | | 3+√73 | |
m∊( |
| ,−1) u (5 , |
| ) |
| | 2 | | 2 | |
to oni musieli uwzględnić
14 cze 20:00
Asmander: Metis czy na pewno masz to dobrze rozwiązane 4m2 −20m +16 ?
14 cze 20:04
ZKS:
Takie coś mi wyszło.
| (m + 1)(m2 − 3m − 16) | |
| < 0 |
| m − 5 | |
14 cze 20:07
Metis: | | m−1 | | m−1 | |
Równanie kwadratowe |
| x2−2(m+2)x+m+4=0 dla |
| ≠0 |
| | m−5 | | m−5 | |
b=−2(m+2)
c=m+4
| | m−1 | |
Δ=[−2(m+2)]2−4* |
| *(m+4)<0 |
| | m−5 | |
14 cze 20:10
Asmander: i tutaj mam pytanie trzeba pomnożyć przez mianownik do
2 czy mianownik po prostu

14 cze 20:12
ZKS:
 Metis
Metis i od razu odpowiedz koledze.

14 cze 20:15
Asmander: no nie śmiejcie się , jestem do tyłu..sporo ...z matmą ..
niech zgadne, że tylko przez mianownik

14 cze 20:17
Metis: Liczę pierwiastki :
(m+1)(m
2−3m−16)=0
| | 3 | | √73 | | 3 | | √73 | |
m=−1 ⋁ m= |
| − |
| ⋁ m= |
| + |
| |
| | 2 | | 2 | | 2 | | 2 | |
Rysuj wykres i odczytaj kiedy <0.
2 warunek:
m≠1 ⋀ m≠5
14 cze 20:17
ZKS:
Nie śmiałem się z Ciebie tylko do
Metis, że jak policzył Δ to i odpowie od razu na
Twoje pytanie.

14 cze 20:19
Metis: Odpowiedziałem już wyżej

14 cze 20:21
Asmander:
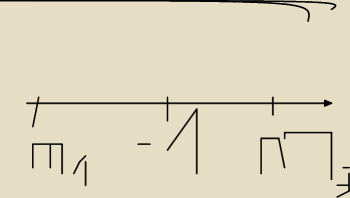
| | 3 | | √73 | | 3 | | √73 | |
m∊(−∞, |
| − |
| u ( |
| + |
| , +∞) |
| | 2 | | 2 | | 2 | | 2 | |
14 cze 20:23
Metis: To nie równanie kwadratowe. Tylko nierówność wielomianowa
142
14 cze 20:24
Metis: *Nierówność kwadratowa

14 cze 20:24
Asmander: chyba będzie mianownik do kwadratu bo w wyniku jest 5...
i powstanie
(m+1)(m2−3m−16)(m−5)=0
14 cze 20:25
Asmander: wiem o tym że jest to nierówność wielomianowa tylko jakoś nie chciało mi sie narysować te fale.
14 cze 20:25
Asmander: albo sam spróbuj rozwiązać tę nierówność
m=−1 , m1=..− , m2=.. +
14 cze 20:26
Asmander:
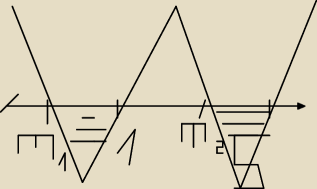
tam w miejsce m2 powinna być 5
14 cze 20:29
Metis: Ale się myle

Myślę o czymś innym i tak to jest.
Poprawiam:
| | 4(m+1)(m2−3m−16) | |
Δ= |
| <0 /*(m−5)2 |
| | m−5 | |
4(m+1)(m
2−3m−16)(m−5)<0
(m+1)(m
2−3m−16)(m−5)<0
Odczytuję pierwiastki:
| | 3 | | √73 | | 3 | | √73 | |
m=−1 v m= |
| − |
| v m= |
| + |
| v m=5 |
| | 2 | | 2 | | 2 | | 2 | |
| | 3−√73 | | 3+√73 | |
Rysujemy wykres i odczytujemy, że m∊( |
| , −1) ∪ (5, |
| ) |
| | 2 | | 2 | |
14 cze 20:33


 Tutaj zachodzi nam takie coś?
Tutaj zachodzi nam takie coś?
 Przepraszam ze się wciąłem ale nie widziałem, że piszesz.
Przepraszam ze się wciąłem ale nie widziałem, że piszesz.



 Metis i od razu odpowiedz koledze.
Metis i od razu odpowiedz koledze. 



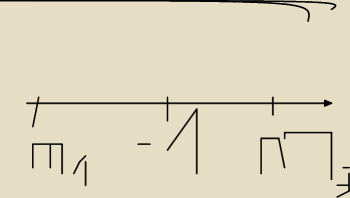

 tam w miejsce m2 powinna być 5
tam w miejsce m2 powinna być 5
 Myślę o czymś innym i tak to jest.
Poprawiam:
Myślę o czymś innym i tak to jest.
Poprawiam: