.. gucio: Punkt (X, Y ) ma rozkład jednostajny na prostokącie o wierzchołkach (0, 0),(2, 0),(2, 1),(0, 1). Znaleźć gęstość, wartość oczekiwaną i wariancję zmiennej losowej Z = X + XY ktoś coś poradzi?

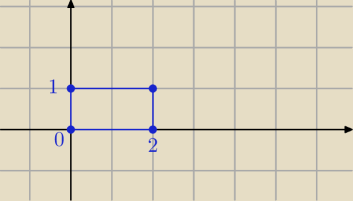
Godzio: Kwadrat = K = { (x,y) ∊ R² : x ∊ [0,2] ∧ y ∊ [0,1] }

	⎧	12 gdy (x,y) ∊ K
f(x,y) =	⎨
	⎩	0 gdy (x,y) ∉ K

	1
E(X + XY) = ∫01∫02(x + xy) *		dxdy =
	2

1		x2
	* ∫01		(1 + y)|02dy =
2		2

1		y2		3
	* ∫01 2(1 + y)dy = (y +		)|01 =
2		2		2

	1
E(X + XY)2 = ∫01∫02x2(1 + y)2 *		dxdy =
	2

1		x3
	∫01		(1 + y)2|02dy =
2		3

1		8
	∫01		(1 + y)2dy =
2		3

4		(1 + y)3		4		8		32
	*		|01 =		*		=
3		3		3		3		3

	32		9		128 − 27		121
Var(X + XY) = E(X + XY)2 − (E(X + XY))2 =		−		=		=
	3		4		4		4

Jakoś tak

Godzio: Na początku oczywiście miałem napisać "Prostokąt"

gucio: a mógłbyś wytłumaczyć skąd się wszystko wzięło w tych całkach?

Godzio: A jaka jest definicja wartości oczekiwanej ?