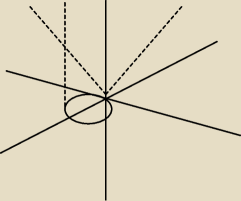
całka powierzchniowa Saris: 6.73 Obliczyć moment bezwładności względem osi OZ jednorodnej powierzchni z=√x²+y² wyciętej walcem x²+y²=2x. ∬_S (x²+y²)*1*dS= (*) − taka to jest całka. teraz pierwsze równanie opisuje stożek ponad płaszczyzną XY (z>=0), a drugie to walec o podstawie r=1 przysunięty o 1 w prawo na osi OX. Nie jestem pewien czy to dobrze robię: Przechodze na walcowe: x=rcost y=rsint z=z (x,y,z)=(x,y,√x²+y²)=(x,y,r) z=r −pi/2<=t<=pi/2 0<=r<=2

	D(x,y)		D(x,z)		D(z,y)
dS=√		+		+		=rsqrt{2}drdt
	D(t,r)		D(t,r)		D(t,r)

(*)=∫^pi/2_pi/2∫²₀ r²*r√2drdt=4sqrt{2}pi To jest zadanie z Krysickiego AM2. Rozwiązanie jest błędne, ale tam połowa rozwiązań jest błedna tylko, że wydaję mi się, że i tak źle to zrobiłem. Ktoś podpowie jak dobrze sparametryzować tą powierzchnię? Bardzo proszę.

kyrtap: jeżeli x2+y2=2x to błędne wyznaczyłeś x i y przechodząc na współrzędne walcowe

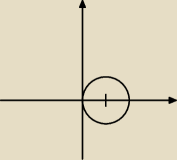
kyrtap: x² + y² = 2x ⇔ x² +y² −2x = 0

⎧	−2a = −2
⎨		⇒ (a = 1 ⋀ b = 0) ⇒ S = (1,0)
⎩	−2b = 0

x² + y² = 2x (rcost)² + (rsint)² = 2rcost r² = 2rcost / :r r = 2cost

	π		π
−		≤ t ≤
	2		2

0 ≤ r ≤ 2cost

Saris: Już do tego doszedłem, ale x/y jest ok tylko przedział r zły. O to chodziło? Dziękuje.

kyrtap: nom

Saris: Ja to zrobiłem tak, że r wychodzi z początku układu więc wpisałem trójkąt oparty na średnicy i policzyłem z cosinusa kąta, bo średnica jest znana.

Saris: Takie zadanko: Obliczyć moment bezw. względem osi OZ jednorodnej części powierzchni kuli x²+y²+z²=a² zawartej między płaszczyznami z=h oraz z=a gdzie 0<h<a. No to powierzchnia ta jest jest częscią sfery od h do a, taka miska. Na początku myślałem, że to jest mniejsza sfera, ale chyba to tak nie działa (bo użyłem wsp. sferycznych i jakieś herezji wychodziły). Doszedłem do wniosku, że trzeba użyć współrzędnych walcowych. x=rcost y=rsint z=z=√a²−r² 0<=t<=2pi (oczywiste) 0<=r<=...

	x2		y2
∫∫S(x2+y2)dS gdzie dS=√1+		+		dxdy (wszystko pod √)
	a2−x2−y2		a2−x2−y2

Czy dobrze rozumuję? Jak wyznaczyć górną granicę r?

Saris: help.

Saris: bump

Saris: .

Saris: ..