ekstrema lokalne damiann1209: Wyznaczyć ekstrema lokalne funkcji: y= x/2 + 2/x Ktoś pomoże z rozwiązaniem?

mol: samemu

PW: Mnie to się kojarzy z powszechnie znaną nierównością

	1
a +		≥ 2
	a

dla a > 0. Dowód polega na wykorzystaniu wiedzy o funkcji kwadratowej. A jak jest dla a < 0?

Janek191:

	x		2
y = f(x) =		+
	2		x

więc

	2
y ' =0,5 −		= 0 ⇔ x2 = 4 ⇔ ( x = − 2 lub x = 2)
	x2

	4x		4
y '' =		=
	x4		x3

więc f ''( − 2) = − 0,5 < 0 − funkcja f ma w punkcie x = − 2 maksimum lokalne równe y{max} = f(− 2) = ... f '' ( 2) = 0,5 > 0 − funkcja f ma w punkcie x = 2 minimum lokalne równe y_min = f(2) = ...

ZKS:

	x		2
Zgodnie z uwagą PW to wykorzystujemy i zauważamy, że funkcja f(x) =		+
	2		x

jest funkcją parzystą, czyli f(−x) = −f(x).

	−x		2		x		2
f(−x) =		+		= −(		+		)
	2		−x		2		x

	x		2
−f(x) = −(		+		).
	2		x

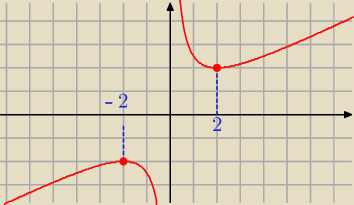
Janek191: f jest funkcją nieparzystą , co widać również na wykresie

ZKS: Oczywiście u mnie winno być " ... nieparzystą, ... ".