 a)
4x2+16x+16≤16
4x2+16x≤0
4x*(x+4)≤0
Miejsca zerowe:
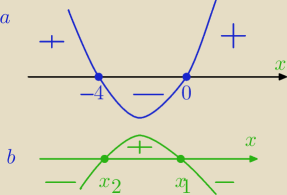
x=0 lub x=−4
x∊<−4,0>
b)−2x2−2√2x+3≤0
Δ=(2√2)2−4*(−2)*3=8+24=32
√32=√16*2=4√2
a)
4x2+16x+16≤16
4x2+16x≤0
4x*(x+4)≤0
Miejsca zerowe:
x=0 lub x=−4
x∊<−4,0>
b)−2x2−2√2x+3≤0
Δ=(2√2)2−4*(−2)*3=8+24=32
√32=√16*2=4√2
| 2√2−4√2 | 2√2+4√2 | |||
x1= | lub x2= | |||
| −2*2 | −2*2 |
| −2√2 | 6√2 | |||
x1= | lub x2= | |||
| −4 | −4 |
| √2 | 3√2 | |||
x1= | lub x2=− | |||
| 2 | 2 |
| 3√2 | √2 | |||
x<− | lub x> | |||
| 2 | 2 |
 a może pan Dionizy życzy sobie np. tak :
a) (2x+4)2≤16 ⇔ |2x+4|≤ 4 /:2 ⇔ |x+2|≤ 2 ⇔
⇔ −2≤ x+2 ≤2 /+(−2) ⇔ −4 ≤ x ≤ 0 ⇔ x∊<−4;0> ;
−−−−−−−−−−−−−−−−−−−−−−−
b) −2x2−2√2x+3≤ 0 /:(−2) ⇔ x2+√2x−32 ≥ 0 ⇔
⇔ x2+2x*12√2+(12√2)2− (12√2)2−32 ≥ 0 ⇔
⇔ (x+12√2)2 ≥ 2 ⇔ |x+12√2| ≥ √2 ⇔
⇔ x+12√2≤ −√2 v x+12√2 ≥√2 ⇔
⇔ x ≤ −32√2 v x ≥ 12√2 ⇔ x∊(−∞;−32√2 > U < 12√2;+∞).
a może pan Dionizy życzy sobie np. tak :
a) (2x+4)2≤16 ⇔ |2x+4|≤ 4 /:2 ⇔ |x+2|≤ 2 ⇔
⇔ −2≤ x+2 ≤2 /+(−2) ⇔ −4 ≤ x ≤ 0 ⇔ x∊<−4;0> ;
−−−−−−−−−−−−−−−−−−−−−−−
b) −2x2−2√2x+3≤ 0 /:(−2) ⇔ x2+√2x−32 ≥ 0 ⇔
⇔ x2+2x*12√2+(12√2)2− (12√2)2−32 ≥ 0 ⇔
⇔ (x+12√2)2 ≥ 2 ⇔ |x+12√2| ≥ √2 ⇔
⇔ x+12√2≤ −√2 v x+12√2 ≥√2 ⇔
⇔ x ≤ −32√2 v x ≥ 12√2 ⇔ x∊(−∞;−32√2 > U < 12√2;+∞). 


