Analityczna-dziwne :( Michcio: Znajdź równania prostych zawierających boki trójkąta ABC wiedząc że B(2,1) jest wierzchołkiem Δ oraz 3x−2y+8=0 i 2x−3y+11=0 to równania wysokości.

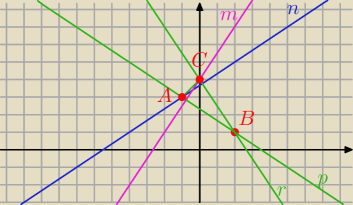
Janek191: m : 3x − 2y + 8 = 0 2 y = 3 x + 8 y = 1,5 x + 4 −−−−−−− n : 2 x − 3 y + 11 = 0 3 y = 2 x + 11

	2		11
y =		x +
	3		3

−−−−−−−−−−−−−

	2
y = −		x + b1 B = ( 2, 1)
	3

	2
1 = −		*2 + b1
	3

	4
1 +		= b1
	3

	7
b1 =
	3

	2		7
p: y = −		x +
	3		3

−−−−−−−−−−−−−−−−−−−−−−−−−− y = −³₂ x + b₂ B =( 2, 1)

	3
1 = −		*2 + b2
	2

b₂ = 4

	3
r: y = −		x + 4
	2

Dokończ: Wyznacz punkty : A i C , a następnie równanie pr. AC

Michcio: Wyszło dzięki