Pole równoległoboku nata: W równoległoboku ABCD (∡ADC >90^o) z punktów B i D poprowadzono wysokości mające długość 60 cm w kierunku krótszych boków. Powstał prostokąt o polu 1500 cm². Następnie z tych samych wierzchołków poprowadzono wysokości mające długość 39 cm na dłuższy bok równoległoboku. Oblicz pole powstałego prostokąta. Proszę o pomoc

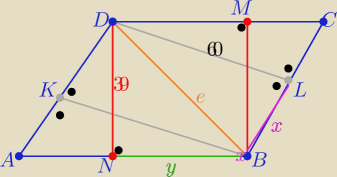
Eta: P(KDLB)= 60*x =1500 ⇒ x=25 Z tw. Pitagorasa w Δ DLB : e= √60²+25²= √4225=65 i z tw. Pitagorasa w ΔDNB : y=√4225−39²= ...=52 P(DNBM)= 39*52= 2028 cm²

Eta: No i jak zwykle tym razem nata czekała, czekała ..... dostała rozwiązanie! ... i ni be ni me ...

nata: Eta bez urazy, ale o 23:30 mózg mi się wyłączył i już poszłam spać. Dziękuję bardzo Ja doszłam do obliczenia przekątnej e , ale jakoś nie dostrzegłam, że jest to też przekątna prostokąta DNBM. Jednak podstawa to porządny rysunek. I tak na koniec: be, me Mam nadzieję, że będę mogła liczyć jeszcze na Twoją pomoc

Eta: Lepiej późno niż wcale dorzucam jeszcze