Szkicowanie wykresu funkcji kumpel: Szkicowanie wykresu funkcji, trzeba wyliczyć: 1. dziedzinę 2. punkty przecięcia ox i oy 3. granicę funkcji 4. pochodną funkcji 5. przedziały monotoniczności 6. ekstrema lokalne funkcji. Z tego musi wyjść tabelka oraz wykres. f(x)=x³−4x²+4x

J: no to działaj ...

kumpel: proszę o pomoc

J: 1) Co można podstawić w miejsce x ?

52: Żartujesz ? Piszesz o ekstremach, a dziedziny nie umiesz wyznaczyć ?

kumpel: d=r, to wiadomo

J: D = R punkt przecięcia z osią OX jaką ma rzędną ?

kumpel: x³−4x²+4x=0

kumpel: wyciągamy x przed nawias tak?

J: dobra .. ⇔ x(x² − 4x + 4) =0 ⇔ x = 0 lub (x −2)² = 0 , czyli ?

kumpel: x=0 v x=2 ?

J: tak ..teraz punkt przecięcia z osią OY ( taki punkt ma odciętą ? )

kumpel: w OY przeważnie wychodzi 0 i w tym przypadku najprawdopodobniej też wychodzi 0

kumpel: x=0

J: przeważnie to pada, albo nie pada to podstaw x = 0 i oblicz y

kumpel: teraz granica

kumpel: no tak, po podstawieniu x=0 wychodzi 0

J: zacznijmy od pochodnej

kumpel: moim zdaniem będzie wyglądać tak: 3x²−4*2*x+4*1=

kumpel: i z tego delta 3x²−8x+1

kumpel: yyyyyy soryy , pomyliło mi się.....

J: tak ... f'(x) = 3x² −8x + 4 liczymy kiedy się zeruje

kumpel: bez delty

J: w pamięci nie policzycz ... licz z Δ

kumpel: pierwiastek z 16

kumpel: teraz x1 i x 2

kumpel: √16=4

J: no to licz ..

kumpel: x1 = 4/6 x2 = 4/6

kumpel: = 2/3 tu i tu

kumpel: nadszedł moment na granicę

J: może być granica , skoro chcesz ... ale miejsca zerowe pochodnej źle..

	4		4
= limx→+∞x3(1 −		+		) = ?
	x		x2

kumpel: ∞

kumpel: i z x→−∞ też ∞

J: OK .. a gdy x → − ∞ ?

kumpel: a co jest nie tak z miejscami zerowymi pochodnej?

J: źle obliczone

kumpel: mógłbyś mi napisać poprawne wyniki w miejscach zerowych pochodnej? ponieważ nie wiem w którym momencie zrobiłem błąd

J:

	2
x = 2 lub x =
	3

kumpel: ok, czyli w x2 pomyliłem znak we wzorze, ale mniejsza, to granice też już mam obliczone

J: teraz ekstrema ... gdzie mogą być ?

kumpel: właśnie tej końcówki nie potrafię a muszę się jej nauczyć

J: ekstrma mogą być tam,gdzie pochodna się zeruje ... warunek: pochodna musi zmieniać znak w tych punktach ... potrafisz naszkicować wykres pochodnej

kumpel:

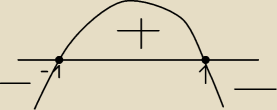
kumpel: o to chodzi?

J: nie ... gałęzie do góry ... i miejsca zerowe: x =2 i x = 2/3

kumpel:

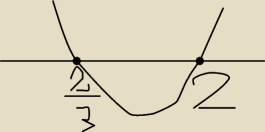
kumpel: o tak

kumpel: i co z tym zrobić?

J:

	2
teraz uważaj ... pochodna zeruje się w punktach: x =		oraz x = 2
	3

w tych punktach zmienia znak, a więc tutaj są ekstrema lokalne tam gdzie pochodna jest dodatnia ( patrz na wykres) funkcja jest rosnąca i odwrotnie ..

	2
zatem w punkcie: x =		funkcja ma ....?
	3

x = 2 funkcja ma ....?

kumpel: ∞ ?

J:

	2
nie łapiesz ... jeśli do punktu x =		funkcja rośnie , a potem maleje,
	3

	2
to w punkcie x =		osiąga maksimum, czy minimum ?
	3

kumpel: minimum

J: pomyśl .. jak idziesz do góry, potem na dół , to byłeś na szczycie, czy na dnie ?

kumpel: na szczycie

kumpel: czyli maksimum

J: brawo ... a w punkcie x = 2 ?

kumpel: minimum, bo byłem na dole i idę do góry

J: no... i masz już kolego wszystko, aby naszkicować wykres tej funkcji

J: a ... jeszcze oblicz te ekstrema: f(2) = ? i f(2/3) = ?

ZKS: Ciekawe tłumaczenie i nawet przedszkolak zrozumie ekstrema.

kumpel: czyli teraz muszę spisać wszystkie wyniki tj. 1. z ox x=0 i x=2 z oy x=0 2. pochodna x1= 2/3 x2= 2 3. Granica ∞ i ∞

kumpel: ale nie widzę jak z tego utworzyć wykres

J: Chciało Ci się to czytać ZKS ....

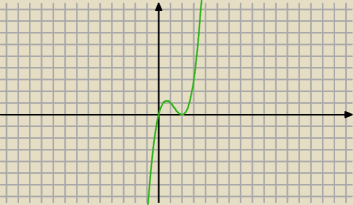
J: mniej więcej tak

ZKS: Jak ktoś ciekawie pisze to z chęcią się to czyta. Dobra nie przeszkadzam i idę dalej projekty tłuc.

kumpel: a w których miejscach są dokładnie poszczególne punkty aby narysować taki wykres?

J: ....powodzenia i pozdrawiam

kumpel: i te ekstrema co wcześniej pisałeś f(2) = ? i f(2/3) = ?

kumpel: No dobra, WIELKIE DZIĘKI ! za pomoc i poświęcony czas

J: stary ... ręce opadają ... przecież wszystko masz policzone ... (zkładam,że policzyłeś f_max = f(2/3) oraz f_min = f(2))

J: tamte życzenia powodzenia kierowałem do ZKS .. ale Tobie też życzę

kumpel: OK, Dzięki za pomoc

ZKS: Dzięki i również pozdrawiam.