Okęgu symetria hs: Wyznacz równanie okręgu, który jest obrazem okręgu k symetrii względem prostej l. (x+2)²+(y−3)²=50 pr. l : 2y−x−2=0

hs:

hs:

hs:

Damian1996: Środkiem danego okręgu jest S=(−2,3) Poprowadź prostą prostopadłą do prostej l, dodatkowo przechodzącą przez punkt S. Punkt przecięcia prostej l i uzyskanej prostej prostopadłej oznaczmy jako P. Dodatkowo oznaczmy środek szukanego okręgu jako S'=(a,b). Zachodzi równość |SP|=|PS'|. Szukane równanie okręgu ma postać (x−a)²+(y−b)²=50. "Przepis" na to zadanie

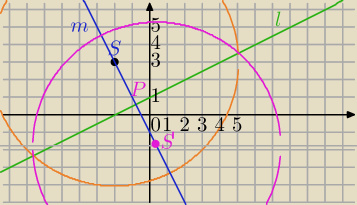
Mila: l: 2y−x−2=0

	1
y=		x+1
	2

S=(−2,3) środek danego okręgu r=√50=5√2 − promień danego okręgu r'=5√2 symetria jest przekształceniem izometrycznym 1) piszemy równanie prostopadłej do prostej l i przechodzącej prze punkt S. m: y=ax+b a=−2 m: y=−2x+b 3=−2*(−2)+b 3=4+b⇔b=−1 m: y=−2x−1 2) punkt przecięcia prostych m i l

	1
−2x−1=		x+1
	2

	4
x=−
	5

	3
y=
	5

	4		3
P=(−		,		)
	5		5

Punkt P jest środkiem odcinka SS', gdzie S'=(x',y') to obraz punktu S w symetrii względem prostej l.

	4		−2+x'		3		3+y'
−		=		i		=
	5		2		5		2

dokończysz?

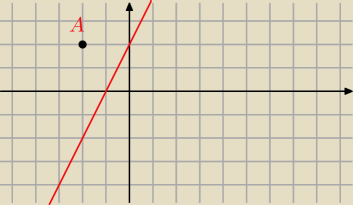
5-latek: Prosta ma równanie y=2x+2 Punkt A ma wspolrzedne A=(−2,2) Wyznacz wspolrzedne obrazu A' punktu A względem tej prostej To nie jest twój przykład tylko chce zobaczyć czy potrafisz to zrobić

hs: Czyli S'=(²₅;−⁹₅) tak ?

hs: Czyli równanie okręgu symetrycznego będzie miało postać ;

	2		9
(x−		)2+(y+		)2=√50
	3		5

Mila:

	2		−9
S'=(		,		)
	5		5

	2		9
(x−		)2+(y+		)2=50
	5		5

hs:

	2
Ojj przepraszam, tam miało być		przy x Dziękuję Faktycznie r2 jest we wzorze ;)
	3

Mila:

2
5