dla jakiej wartości parametru k styczne john2: Oblicz, dla jakiej wartości parametru k styczne do okręgu (x − 1)² + (y − 2)² = 9 przecinają się pod kątem 60⁰ i przechodzą przez punkt A należący do prostej y = 3x + k. Oto rozwiązanie wraz z rysunkiem przedstawione w książce, którego nie rozumiem: Zauważmy, że skoro promień okręgu wynosi 3, a kąt 60⁰ został podzielony dwusieczną SA na dwa równe kąty po 30⁰, to |SA| = 6 z zależności trójkąta o kątach (30⁰, 60⁰, 90⁰). Korzystamy ze wzoru na odległość punktu od prostej

	|Ax0 + By0 + C|
|d| =
	√A2 + B2

W naszym przypadku układamy równanie z odległością punktu S od prostej y = 3x + k Zamieniamy wzór prostej na postać ogólną 3x − y + k = 0 s(x₀,y₀) = (1,2) Po podstawieniu:

|1 + k|
	= 6
√10

ostatecznie k = 6√10 − 1 lub k = −6√10 − 1 MOJE PYTANIE: Na jakiej podstawie stosujemy wzór na odległość punktu od prostej? Czy aby odcinek, który tworzy tę odległość, nie musi być prostopadły do tej prostej? Jeśli tak, to skąd wiemy, że tutaj tak jest?

john2: Mógłby ktoś zasugerować ewentualnie inne rozwiązanie?

J: zauważ,że wszystkie punkty w których styczne się przecinają, leżą na okręgu o środku S(1,2) i promieniu r = 6. Aby taki punkt należał do danej prostej, musi ona być styczna do tego okręgu, czyli odległa od środka o promień r = 6

john2: Mógłbyś wyjaśnić, z czego to wynika, że punkty, gdzie styczne się przecinają, leżą na okręgu o promieniu 6?

J: przecież widzisz,że jest to trójkąt prostokątny 30,60,90 więc przeciwprostokątna IASI = 6

john2: Chyba widzę, dziękuję.

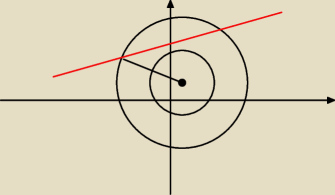
john2: J, proszę o jeszcze moment cierpliwości dla mnie, bo teraz nie mogę zrozumieć sformułowania: "Aby taki punkt należał do danej prostej, musi ona być styczna do tego okręgu" Dlaczego ta prosta musi być styczną, a nie np. sieczną, jak na rysunku. Wiem, że równanie y = 3x + k sugeruje, że jest ona bardziej stroma, ale czy mogę mieć pewność, że współczynnik a = 3 wystarczy, żeby nie przeciąć tego dużego okręgu dwa razy?

J: Chyba masz rację ... Teraz się na tym zastanowiłem i widzę,że nie ma żadnego uzasadnienia ( przy tak sformułowanej treści zadania), aby prosta y = 3x + k była styczna do okręgu, na którym leżą punkty przecięcia się stycznych. Zadanie wymaga jedynie, aby taki punkt należał do tej prostej. Sprawdź jeszcze raz dokładnie treść zadania .. A może ktoś z kolegów z forum wypowie sie w tej kwestii

john2: Obawiam się, że treść się zgadza Zadanie z "Jak zdać maturę z matematyki na poziomie rozszerzonym" Pana Dariusza Kulmy.

J: Może ktoś jeszcze się wypowie ... poczekajmy. Moim zdaniem takich prostych jest nieskończenie wiele, ale mogę sie mylić Jeszcze jedno ..., czy rysunek jaki pokazałeś ,jest taki jak w książce ?

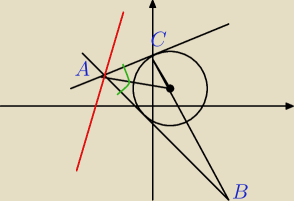
john2: W zasadzie to tak wygląda. Tylko jest on już częścią rozwiązania, nie treści. Trójkąt ABC jest prostokątny. Na zielono są dwa kąty po 30 stopni. Czerwona to prosta y = 3x + k.

J: .. zadanie jest w takim razie knotem ... treść zadania w żaden sposób nie ogranicza nam położenia stycznych , poza oczywiście kątem 60⁰,który jestnarzucony ... jeśli tak, to przyjmijmy ich położenie, tak jak na rysunku .. obracamy czerwoną prostą ( y = 3x + k ) ,gdzie środkiem obrotu jest punkt A... punkt A cały czas spełnia warunki zdania ( należy do prostej), ale odległość prostej od środka okręgu S( 1,2) się zmienia ... ergo: takich prostych jest nieskończenie wiele

J: ..trochę się zagalopowałem ... prostej czerwonej nie mozemy obracać, bo a = 3 , ale możemy ją równolegle przesuwać .... jeśli ją przesuniemy, to zwsze tak obrócimy styczne, aby ich punkt przecięcia znalazł się na czerwonej prostej ( pomijając takie przesunięcie, że jej odległość od środka okręgu przekroczy: d = 6)

john2: Od początku mi się to zadanie nie podobało. Coś jest na rzeczy, bo ja to widzę tak. Biorąc różne proste o tym samym współczynniku kierunkowym i nie wiedząc gdzie dokładnie na nich ma leżeć ten punkt A, faktycznie na każdej z tych prostych znajdzie się taki punkt A, gdzie przechodzące przez niego styczne do okręgu będą się przecinały pod danym kątem.

john2: No właśnie. Chyba zagadka rozwiązana. Dzięki.