Przedzialy monotonnicznisci funkcji i ich extrema Sara: Przedzialy monotonnicznisci funkcji i ich extrema z gory dzieki za pomoc F (x) = 1/2x⁴+x²−3 F (x)= (−x²+9)/ (x+5)

J: trzeba zacząć od policzenia pochodnej

Sara: To wiem ale jak bys mogl obloczenia pokazac dla pewnosci i nauki przy okazji

J: spróbuj sama ... poprawimy 1) pochodna , to pochodna sumy trzech funkcji

Sara: To ja powiem co chce robic najpierw : Pochodna funkcji Nierownosc f (x) >=0 Rozwiazac nierownoscf (x)<=0 I co dalej ?

J: jeśli pochodna zeruje się w punkcie: x₀ oraz zmienia znak w tym punkcie to znaczy,że posiada eksteremum w punkcie x₀ w przedziałach gdzie f'(x) > 0 funkcja jest rosnąca i odwrotnie pokaż pochodną ..

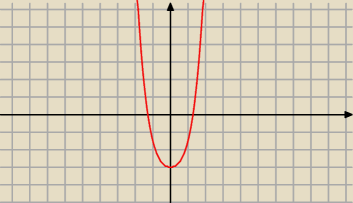
Janek191: 1) Df = ℛ 2) f '(x) = 0,5* 4 x³ + 2 x = 2 x³ + 2x = 2 x*( x² + 1) = 0 ⇔ x = 0 3) f ' (x) = 6 x + 2 f '' (0) = 6*0 + 2 = 2 > 0 więc funkcja f ma w punkcie x = 0 minimum lokalne równe y_min = f(0) = − 3 4) Dla x < 0 jest f '(x) < 0 więc wtedy f maleje Dla x > 0 jest f' (x) > 0 więc wtedy f rośnie Patrz też na wykres

Janek191: Zrób II przykład

J: poczeka,aż Ty to zrobisz

Janek191: Tam w 3) powinno być f ''(x) = 6 x + 2 − II pochodna funkcji f

Janek191: O pomyliłem się , ale to nie zmienia istoty rozwiązania. powinno być f ''(x) = 6 x² + 2 f ''(0) = 2 > 0 itd.