Trygonometria
Michcio: Przyprostokątne Δ prostokątnego mają długość 3 i
√3. Naprzeciwko boku długości 3 leży kąt α,
naprzeciwko boku długości
√3 leży kąt β. Udowodnij bez użycia wzoru na kosinus różnicy
| | √3 | |
kątów, że cos (α−β)= |
| |
| | 2 | |
11 cze 02:58
Kacper:
Ile jest α? a ile β?
11 cze 07:05
Bogdan:
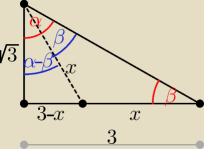
| | √3 | |
(√3)2 + (3 − x)2 = x2 ⇒ x = ... cos(α − β) = |
| |
| | x | |
11 cze 08:05
Eta:
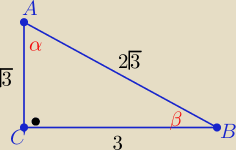
Można też tak:
Jeżeli taka równość zachodzi
| | √3 | |
to cos(α−β)= |
| ⇒ α−β= 30o i α+β=90o ⇒ 2α=120o ⇒ α=60o i β= 30o |
| | 2 | |
mamy trójkąt "ekierkę" o kątach 90
o, 30
o, 60
o
| | √3 | |
zatem |AB|= 2√3 czyli cos30o= cos(α−β)= |
| |
| | 2 | |
c.n.u
12 cze 01:24