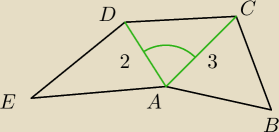
Pytanie Michcio: Błąd w odpowiedziach Oblicz pole pięciokąta wiedząc że ma boki jednakowej długości AD = 2 AC = 3 |∡CAD| = 60 stopni Rozwiązanie

	1
Pole ΔDAC =		*2*3*sin 60 = 1,5√3
	2

Z Tw. kosinusów CD = √10 (Nie wiem jak policzyć bok bez tw.kosinusów niestety) Czyli każdy bok ma √10

	4
Wychodzi mi pole 1,5√3+3+		√31
	3

Natomiast w odpowiedziach jest 1,5√3+√6+0,75√19

Damian1996: Błędnie policzyłeś długość boku CD z tw. cosinusów. Mi wyszło |CD|=√7

Janek191: Tak: I CD I = √7

Michcio: Faktycznie, to by wyjaśniało ten błąd. Wtedy wychodzi odp. ok No dobrze a można jakoś dojść do tego boku nie mieszając w to w/w twierdzenie ? Bo zadanie pochodzi ze zbiorku dla I klasy