Prawdopodobieństwo losowanie bez zwracania sprawdzenie
PablooPom: Do sprawdzenia, trudniejsze:
Spośród 3 monet jednozłotowych, 5 dwuzłotowych i 4 pięciozłotowych losujemy kolejno bez
zwracania 2 monety. Oblicz prawdopodobieństwo wylosowania w sumie więcej niż 3 złotych.
Czyli jedną z monet musi być pięciozłotówka? tak rozumowałem
3 monety − 1zł
5 monet − 2zł
4 monety − 5zł
|Ω| = 3*5*4 = 60
|A| = 3*4 + 5*4 = 32
P|A| = 3260 = 815
Wydaje mi się że coś poknociłem
10 cze 21:24
Mila:
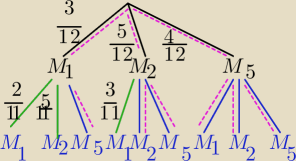
A− wylosowano więcej niż 3 złote
A' − wylosowano kwotę mniejszą lub równą 3 złote
| | 3 | | 2 | | 3 | | 5 | | 5 | | 3 | |
P(A')= |
| * |
| + |
| * |
| + |
| * |
| = |
| | 12 | | 11 | | 12 | | 11 | | 12 | | 11 | |
| | 6 | | 15 | | 15 | | 36 | | 3 | |
= |
| + |
| + |
| = |
| = |
| |
| | 12*11 | | 12*11 | | 12*11 | | 12*11 | | 11 | |
=========================
Albo tak:
|Ω|=12*11
Masz zbiory: Z
1={1,1,1}, Z
2={2,2,2,2,2}, z
5={5,5,5,5}
Zdarzenia sprzyjające :
(1,5),(2,5),(2,2),(5,1),(5,2),(5,5)
|A|=3*4+5*4+5*4+4*3+4*5=96
=======================
Albo tak:
A'
Zdarzenia sprzyjające.
(1,1),(1,2)(2,1)
|A'=3*2+3*5+5*3=36 (36+96=132)
===========
10 cze 22:11
Jamm: "Albo tak:
|Ω|=12*11
Masz zbiory: Z1={1,1,1}, Z2={2,2,2,2,2}, z5={5,5,5,5}
Zdarzenia sprzyjające :
(1,5),(2,5),(2,2),(5,1),(5,2),(5,5)
|A|=3*4+5*4+5*4+4*3+4*5=96"
^^ w tym chyba jest coś nie tak? bo w |A| by wyszło 84
10 cze 22:29
Jamm: dobra wieeem

brakuje tam ostatniego z (5,5) czyli 4*3, to jest to brakujące 12

10 cze 22:37
Mila:
Tak, nie przepisałam z kartki, dziękuję za poprawkę.

10 cze 22:42
Jamm: To ja dziękuję, tyle już się nauczyłem dzięki Tobie.. WIELKIE DZIĘKI

10 cze 22:44
Mila:

10 cze 22:46
 A− wylosowano więcej niż 3 złote
A' − wylosowano kwotę mniejszą lub równą 3 złote
A− wylosowano więcej niż 3 złote
A' − wylosowano kwotę mniejszą lub równą 3 złote
 brakuje tam ostatniego z (5,5) czyli 4*3, to jest to brakujące 12
brakuje tam ostatniego z (5,5) czyli 4*3, to jest to brakujące 12 


